最小二乗法を用いた二次ベジェ曲線による三次ベジェ曲線の近似
二次ベジェ曲線の式
二次ベジェ曲線の式を以下の通りです。
$$ \begin{align} \begin{split} &x(t)=a_xt^2+b_xt+c_x\\ &y(t)=a_yt^2+b_yt+c_y \end{split} \tag{1} \end{align} $$ $$ \begin{align} \begin{split} &a_x=(P_{0x}-2P_{1x}+P_{2x})\\ &b_x=2(-P_{0x}+P_{1x})\\ \end{split} \tag{2} \end{align} $$ $$ \begin{align} \begin{split} &a_y=(P_{0y}-2P_{1y}+P_{2y})\\ &b_y=2(-P_{0y}+P_{1y}) \end{split} \tag{3} \end{align} $$制約なし
特に制約条件を設けずに近似式を求めます。二次ベジェ曲線と三次ベジェ曲線上の点\((x_i,y_i)\)との距離の二乗\(d_i^2\)の総和は
$$ \sum_{i=0}^nd_i^2=\sum_{i=0}^n(a_xt_i^2+b_xt_i+c_x-x_i)^2+\sum_{i=0}^n(a_yt_i^2+b_yt_i+c_y-y_i)^2 \tag{4} $$となります。この式を展開すると以下の式となります。
$$ \begin{split} \begin{align} \sum_{i=0}^nd_i^2 &=\sum_{i=0}^n\left[ a_x^2t_i^4+2a_xb_xt_i^3+(2a_xc_x-2a_xx_i+b_x^2)t_i^2 \right.\\ &\hspace{40px} \left.+(2b_xc_x-2b_xx_i)t_i-2c_xx_i+c_x^2+x_i^2 \right]\\ &+\sum_{i=0}^n\left[ a_y^2t_i^4+2a_yb_yt_i^3+(2a_yc_y-2a_yy_i+b_y^2)t_i^2 \right.\\ &\hspace{40px} \left.+(2b_yc_y-2b_yy_i)t_i-2c_yy_i+c_y^2+y_i^2 \right]\\ \end{align} \end{split} \tag{5} $$ここで
$$ D=\sum_{i=0}^nd_i^2 \tag{6} $$と置きます。以下の式を満たす場合、\(D\)が最小となります。この式を用いて、二次ベジェ曲線の係数\(a_x,b_x,c_x,a_y,b_y,c_y\)を求めます。
$$ \begin{align} &\frac{\partial D}{\partial a_x}=0, \space \frac{\partial D}{\partial b_x}=0, \space \frac{\partial D}{\partial c_x}=0 \tag{7}\\ &\frac{\partial D}{\partial a_y}=0, \space \frac{\partial D}{\partial b_y}=0, \space \frac{\partial D}{\partial c_y}=0 \tag{8}\\ \end{align} $$式\((7)\)より以下の式が得られます。
$$ \begin{align} &\sum_{i=0}^n\left[ 2a_xt_i^4+2b_xt_i^3+(2c_x-2x_i)t_i^2 \right] =0\\ \Leftrightarrow\hspace{10px} &a_x\sum{t^4}+b_x\sum{t^3}+c_x\sum{t^2}-\sum{xt^2}=0 \tag{9} \end{align} $$ $$ \begin{align} &\sum_{i=0}^n\left[ 2a_xt_i^3+2b_xt_i^2+(2c_x-2x_i)t_i \right] =0\\ \Leftrightarrow\hspace{10px} &a_x\sum{t^3}+b_x\sum{t^2}+c_x\sum{t}-\sum{xt}=0 \tag{10} \end{align} $$ $$ \begin{align} &\sum_{i=0}^n\left[ 2a_xt_i^2+2b_xt_i+2c_x-2x_i \right] =0\\ \Leftrightarrow\hspace{10px} &a_x\sum{t^2}+b_x\sum{t}+c_x\sum{1}-\sum{x}=0 \tag{11} \end{align} $$式\((9)\)、式\((10)\)及び式\((11)\)より\(a_x\)、\(b_x\)及び\(c_x\)を行列を用いて求めます。
$$ \begin{pmatrix} \sum{t^4} & \sum{t^3} & \sum{t^2}\\ \sum{t^3} & \sum{t^2} & \sum{t}\\ \sum{t^2} & \sum{t} & \sum{1} \end{pmatrix} \begin{pmatrix} a_x\\ b_x\\ c_x \end{pmatrix} = \begin{pmatrix} \sum{xt^2}\\ \sum{xt}\\ \sum{x} \end{pmatrix} \tag{12} $$これより
$$ \begin{pmatrix} a_x\\ b_x\\ c_x \end{pmatrix} = \begin{pmatrix} \sum{t^4} & \sum{t^3} & \sum{t^2}\\ \sum{t^3} & \sum{t^2} & \sum{t}\\ \sum{t^2} & \sum{t} & \sum{1} \end{pmatrix}^{-1} \begin{pmatrix} \sum{xt^2}\\ \sum{xt}\\ \sum{x} \end{pmatrix} \tag{13} $$となります。逆行列\(A^{-1}\)は行列式\(|A|\)と余因子行列\(\tilde{A}\)を用いて求めることができます。
$$ A^{-1}=\frac{1}{|A|}\tilde{A} \tag{14} $$ここで
$$ A=\begin{pmatrix} \sum{t^4} & \sum{t^3} & \sum{t^2}\\ \sum{t^3} & \sum{t^2} & \sum{t}\\ \sum{t^2} & \sum{t} & \sum{1} \end{pmatrix} \tag{15} $$とおくと、\(|A|\)は
$$ \begin{align} |A|&=\sum{t^4}\sum{t^2}\sum{1}+2\sum{t^3}\sum{t^2}\sum{t}\\ &-\Bigl(\sum{t^2}\Bigr)^3-\Bigl(\sum{t^3}\Bigr)^2\sum{1}-\sum{t^4}\Bigl(\sum{t}\Bigr)^2 \end{align} \tag{16} $$また、\(\tilde{A}\)は
$$ \tilde{A}= \begin{pmatrix} \sum{t^2}\sum{1}-\Bigl(\sum{t}\Bigr)^2 & \sum{t^2}\sum{t}-\sum{t^3}\sum{1} & \sum{t^3}\sum{t}-\Bigl(\sum{t^2}\Bigr)^2\\ \sum{t^2}\sum{t}-\sum{t^3}\sum{1} & \sum{t^4}\sum{1}-\Bigl(\sum{t^2}\Bigr)^2 & \sum{t^3}\sum{t^2}-\sum{t^4}\sum{t}\\ \sum{t^3}\sum{t}-\Bigl(\sum{t^2}\Bigr)^2 & \sum{t^3}\sum{t^2}-\sum{t^4}\sum{t} & \sum{t^4}\sum{t^2}-\Bigl(\sum{t^3}\Bigr)^2 \end{pmatrix} \tag{17} $$となります。よって、\(a_x\)、\(b_x\)及び\(c_x\)は
$$ \begin{align} a_x&=\frac{1}{|A|}\Bigl\lbrace\Bigl[\sum{t^2}\sum{1}-\Bigl(\sum{t}\Bigr)^2\Bigr]\sum{xt^2}\\ &\hspace{60px}+\Bigl[\sum{t^2}\sum{t}-\sum{t^3}\sum{1}\Bigr]\sum{xt}\\ &\hspace{75px}+\Bigl[\sum{t^3}\sum{t}-\Bigl(\sum{t^2}\Bigr)^2\Bigr]\sum{x}\Bigr\rbrace \end{align} \tag{18} $$ $$ \begin{align} b_x&=\frac{1}{|A|}\Bigl\lbrace\Bigl[\sum{t^2}\sum{t}-\sum{t^3}\sum{1}]\sum{xt^2}\\ &\hspace{60px}+\Bigl[\sum{t^4}\sum{1}-\Bigl(\sum{t^2}\Bigr)^2]\sum{xt}\\ &\hspace{75px}+\Bigl[\sum{t^3}\sum{t^2}-\sum{t^4}\sum{t}]\sum{x}\Bigr\rbrace \end{align} \tag{19} $$ $$ \begin{align} c_x&=\frac{1}{|A|}\Bigl\lbrace\Bigl[\sum{t^3}\sum{t}-\Bigl(\sum{t^2}\Bigr)^2]\sum{xt^2}\\ &\hspace{60px}+\Bigl[\sum{t^3}\sum{t^2}-\sum{t^4}\sum{t}]\sum{xt}\\ &\hspace{75px}+\Bigl[\sum{t^4}\sum{t^2}-\Bigl(\sum{t^3}\Bigr)^2]\sum{x}\Bigr\rbrace \end{align} \tag{20} $$と求まります。同様に\(a_y\)、\(b_y\)及び\(c_y\)は
$$ \begin{align} a_y&=\frac{1}{|A|}\Bigl\lbrace\Bigl[\sum{t^2}\sum{1}-\Bigl(\sum{t}\Bigr)^2\Bigr]\sum{yt^2}\\ &\hspace{60px}+\Bigl[\sum{t^2}\sum{t}-\sum{t^3}\sum{1}\Bigr]\sum{yt}\\ &\hspace{75px}+\Bigl[\sum{t^3}\sum{t}-\Bigl(\sum{t^2}\Bigr)^2\Bigr]\sum{y}\Bigr\rbrace \end{align} \tag{21} $$ $$ \begin{align} b_y&=\frac{1}{|A|}\Bigl\lbrace\Bigl[\sum{t^2}\sum{t}-\sum{t^3}\sum{1}]\sum{yt^2}\\ &\hspace{60px}+\Bigl[\sum{t^4}\sum{1}-\Bigl(\sum{t^2}\Bigr)^2]\sum{yt}\\ &\hspace{75px}+\Bigl[\sum{t^3}\sum{t^2}-\sum{t^4}\sum{t}]\sum{y}\Bigr\rbrace \end{align} \tag{22} $$ $$ \begin{align} c_y&=\frac{1}{|A|}\Bigl\lbrace\Bigl[\sum{t^3}\sum{t}-\Bigl(\sum{t^2}\Bigr)^2]\sum{yt^2}\\ &\hspace{60px}+\Bigl[\sum{t^3}\sum{t^2}-\sum{t^4}\sum{t}]\sum{yt}\\ &\hspace{75px}+\Bigl[\sum{t^4}\sum{t^2}-\Bigl(\sum{t^3}\Bigr)^2]\sum{y}\Bigr\rbrace \end{align} \tag{23} $$となります。
グラフ
分割なし
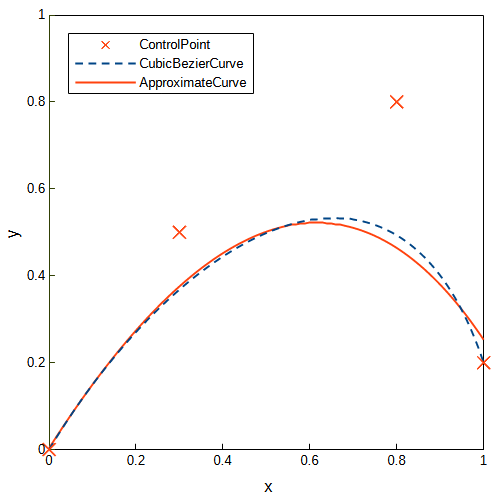
コントロールポイントを\(P_0=(0, 0)\), \(P_1=(0.3, 0.5)\), \(P_2=(0.8, 0.8)\), \(P_3=(1.0, 0.2)\)としたときの三次ベジェ曲線と近似二次ベジェ曲線のグラフを以下に示します。近似二次ベジェ曲線を求める際の\(t\)は三次ベジェ曲線の\(t\)をそのまま使用しています。\(x=0.6\)以降は大きな誤差が生じています。
二分割
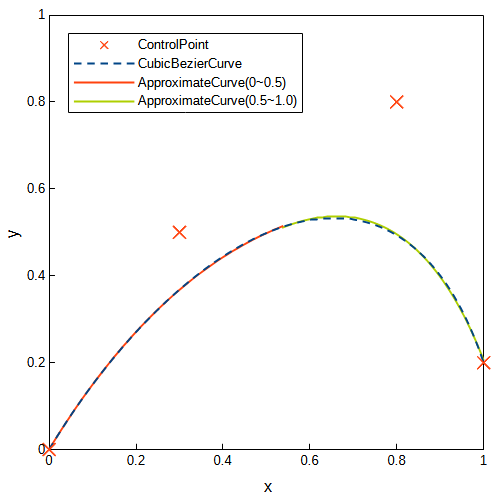
三次ベジェ曲線を分割し、それぞれの区間を異なる二次ベジェ曲線で近似しました。分割なしの場合より、誤差が少なくなっています。
四分割
さらに、三次ベジェ曲線を四分割し、近似二次ベジェ曲線を求めました。きれいに近似できていることが分かります。
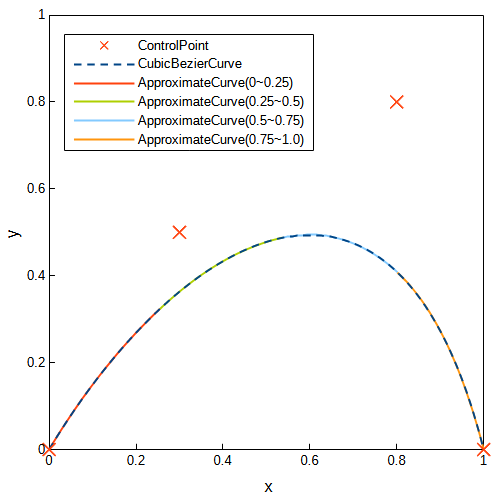
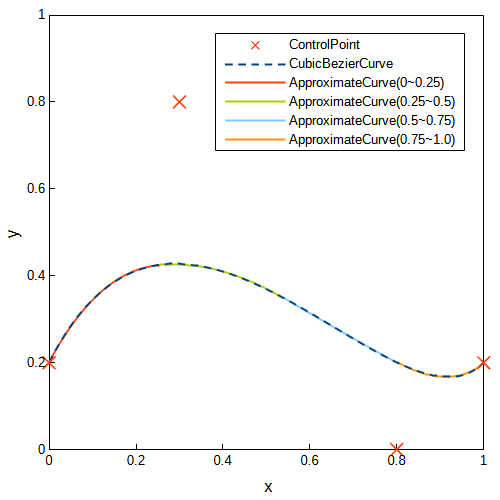
また、コントロールポイントを\(P_0=(0, 0.2)\), \(P_1=(0.3, 0.8)\), \(P_2=(0.8, 0)\), \(P_3=(1.0, 0.2)\)とした場合の近似二次ベジェ曲線を求めました。先ほどと同様にきれいに近似できています。
両端固定
求める近似二次ベジェ曲線の両端と三次ベジェ曲線の両端の位置が一致することを条件に追加します。式\((5)\)へ式\((2)\)及び式\((3)\)を代入すると
$$ \begin{split} \begin{align} &D=(P_{0x}^2-4P_{0x}P_{1x}+2P_{0x}P_{2x}+4P_{1x}^2-4P_{1x}P_{2x}+P_{2x}^2)\sum{t^4}\\ &\hspace{20px} +4(-P_{0x}^2+3P_{0x}P_{1x}-2P_{1x}^2-P_{0x}P_{2x}+P_{1x}P_{2x})\sum{t^3}\\ &\hspace{20px} +(6P_{0x}^2-12P_{0x}P_{1x}+2P_{0x}P_{2x}+4P_{1x}^2)\sum{t^2}\\ &\hspace{20px} -2(P_{0x}-2P_{1x}+P_{2x})\sum{xt^2}+4(-P_{0x}^2+P_{0x}P_{1x})\sum{t}\\ &\hspace{20px} -4(-P_{0x}+P_{1x})\sum{xt}-2P_{0x}\sum{x}+\sum{x^2}+P_{0x}^2\\ &\hspace{20px} +(P_{0y}^2-4P_{0y}P_{1y}+2P_{0y}P_{2y}+4P_{1y}^2-4P_{1y}P_{2y}+P_{2y}^2)\sum{t^4}\\ &\hspace{20px} +4(-P_{0y}^2+3P_{0y}P_{1y}-2P_{1y}^2-P_{0y}P_{2y}+P_{1y}P_{2y})\sum{t^3}\\ &\hspace{20px} +(6P_{0y}^2-12P_{0y}P_{1y}+2P_{0y}P_{2y}+4P_{1y}^2)\sum{t^2}\\ &\hspace{20px} -2(P_{0y}-2P_{1y}+P_{2y})\sum{yt^2}+4(-P_{0y}^2+P_{0y}P_{1y})\sum{t}\\ &\hspace{20px} -4(-P_{0y}+P_{1y})\sum{yt}-2P_{0y}\sum{y}+\sum{y^2}+P_{0y}^2 \end{align} \end{split} \tag{20} $$となります。以下のを満たす場合、\(D\)が最小となります。この式を用いて\(P_{1x}\)を求めます。
$$ \frac{\partial D}{\partial P_{1x}}=0 \tag{21} $$式\((20)\)より
$$ \begin{align} &\frac{\partial D}{\partial P_{1x}}=(-4P_{0x}+8P_{1x}-4P_{2x})\sum{t^4} +4(3P_{0x}-4P_{1x}+P_{2x})\sum{t^3}\\ &\hspace{60px} +(-12P_{0x}+8P_{1x})\sum{t^2} +4\bar{xt^2}+4P_{0x}\sum{t}-4\sum{xt} \end{align} \tag{22} $$となります。よって\(P_{1x}\)は
$$ P_{1x}= \frac{ (P_{0x}+P_{2x})\sum{t^4}-(3P_{0x}+P_{2x})\sum{t^3}+3P_{0x}\sum{t^2}-\sum{xt^2}-P_{0x}\sum{t}+\sum{xt} }{ 2(\sum{t^4}-2\sum{t^3}+\sum{t^2}) } \tag{23} $$と求まります。同様に\(P_{1y}\)は
$$ P_{1y}= \frac{ (P_{0y}+P_{2y})\sum{t^4}-(3P_{0y}+P_{2y})\sum{t^3}+3P_{0y}\sum{t^2}-\sum{yt^2}-P_{0y}\sum{t}+\sum{yt} }{ 2(\sum{t^4}-2\sum{t^3}+\sum{t^2}) } \tag{24} $$となります。
グラフ
分割なし
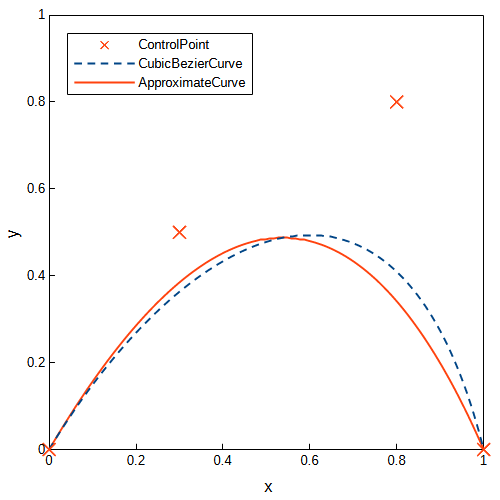
コントロールポイントを\(P_0=(0, 0)\), \(P_1=(0.3, 0.5)\), \(P_2=(0.8, 0.8)\), \(P_3=(1.0, 0.2)\)としたときの三次ベジェ曲線と近似二次ベジェ曲線のグラフを以下に示します。始点と終点が一致している代わりに制約なしの場合より誤差が大きくなっています。
二分割
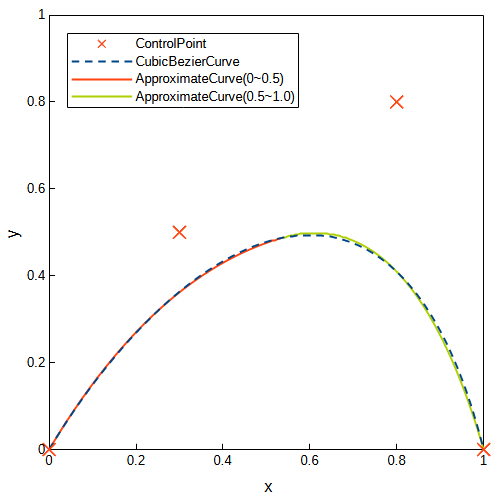
三次ベジェ曲線を分割し、それぞれの区間を異なる二次ベジェ曲線で近似しています。分割なしの場合より、誤差が少なくなっています。
四分割
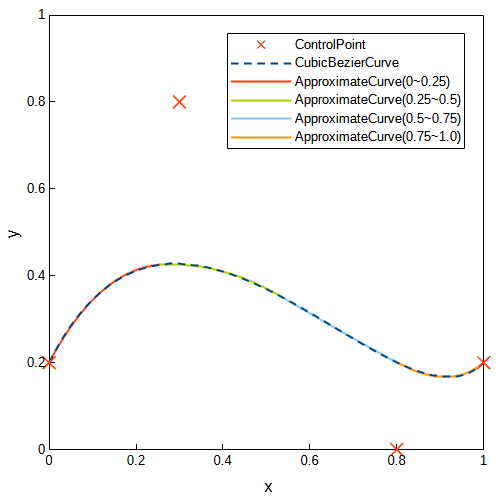
三次ベジェ曲線を四分割し、近似二次ベジェ曲線を求めました。きれいに近似できていることが分かります。

コントロールポイントを\(P_0=(0, 0.2)\), \(P_1=(0.3, 0.8)\), \(P_2=(0.8, 0)\), \(P_3=(1.0, 0.2)\)とした場合でもきれいに近似できています。
-
前の記事
二次ベジェ曲線の対称性 2023.07.28
-
次の記事
三次ベジェ曲線の最接近点(近似二次ベジェ曲線を利用) 2023.12.10




コメントを書く