4点を通る三次ベジェ曲線

三次ベジェ曲線は二つの端点と二つの方向点によって形が決まります。この場合、ベジェ曲線は方向点を通りません。そこで、二つの端点とその間にある二つの点から方向点を決定し、この方向点を用いて4点を通る三次ベジェ曲線を求めました。
式
三次ベジェ曲線は以下の式で表されます。\(C_0\)及び\(C_3\)は端点、\(C_1\)及び\(C_2\)は方向点です。
$$ \begin{align} &P = (1-t)^3C_0 + 3(1 – t)^2tC_1 + 3(1 – t)t^2C_2 + t^3C_3 \tag{1}\\ \end{align} $$式\((1)\)より\(t=0\)及び\(t=1\)では
$$ \begin{align} &C_0 = P_0 \tag{2}\\ &C_3 = P_3 \tag{3}\\ \end{align} $$となります。また\(t=t_1\)のとき\(P=P_1\)及び\(t=t_2\)のとき\(P=P_2\)とすると式\((1)\)より、\(P_1\)及び\(P_2\)は式\((4)\)、\((5)\)となります。
$$ \begin{align} &P_1 = (1-t_1)^3C_0 + 3(1 – t_1)^2t_1C_1 + 3(1 – t_1)t_1^2C_2 + t_1^3C_3 \tag{4}\\ &P_2 = (1-t_2)^3C_0 + 3(1 – t_2)^2t_2C_1 + 3(1 – t_2)t_2^2C_2 + t_2^3C_3 \tag{5}\\ \end{align} $$これより\(C_1\)及び\(C_2\)は
$$ \begin{align} &C_2 = \frac{P_1 – aP_0 – dP_3 – bC_1}{c} \tag{6}\\ &C_1 = \frac{P_2 – eP_0 – hP_3 – gC_2}{f} \tag{7}\\ \end{align} $$となります。ただし
$$ \begin{align} &a = (1 – t_1)^3,\ b = 3(1 – t_1)^2t_1,\ c= 3(1 – t_1)t_1^2,\ d = t_1^3 \tag{8}\\ &e = (1 – t_2)^3,\ f= 3(1 – t_2)^2t_2,\ g = 3(1 – t_2)t_2^2,\ h = t_2^3 \tag{9}\\ \end{align} $$です。式\((6)\)及び式\((7)\)より\(C_1\)は式\((10)\)となります。
$$ \begin{align} &C_1 = \frac{(ag – ce)P_0 – gP_1 + cP_2 + (dg – ch)P_3}{cf – bg} \tag{10}\\ \end{align} $$以上の式より、二つの方向点\(C_1\)及び\(C_2\)を求めることができます。
グラフ
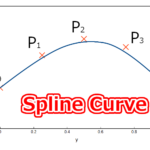
以下の頂点を用いて三次ベジェ曲線を求め、グラフを作成しました。
$$ \begin{align} &P_0(0, 0)\\ &P_1(3, 0.1),\ t_1=0.3\\ &P_2(6, 0.3),\ t_2=0.6\\ &P_3(10, 0)\\ \end{align} $$
以上のグラフに示すように指定された4点を通るベジェ曲線が得られました。ただし、\(t_1\)及び\(t_2\)を以下のように変更すると
$$ t_1=0.1,\ t_2=0.8 $$
となります。\(t_1\)及び\(t_2\)の値によってはきれいな曲線にならないことがあるようです。
-
前の記事
CustomVolumeParameterとインスペクターのエディタ拡張(Volume Component) 2023.03.21
-
次の記事
ベジェ曲線の最接近点 2023.05.03




コメントを書く