三次ベジェ曲線の最接近点(近似二次ベジェ曲線を利用)
- 2023.12.10
- Math
三次ベジェ曲線の最接近点
最小二乗法を用いた二次ベジェ曲線による三次ベジェ曲線の近似によって求めた四つの近似二次ベジェ曲線における最接近点を求め、その結果から三次ベジェ曲線における最接近点を求めます。
step1
最小二乗法を用いた二次ベジェ曲線による三次ベジェ曲線の近似を用いて四つに区切った三次ベジェ曲線において、それぞれの区間に対し近似二次ベジェ曲線を求めます。二次ベジェ曲線は以下の通りです。
$$ \begin{align} \begin{split} &x(t)=a_xt^2+b_xt+c_x\\ &y(t)=a_yt^2+b_yt+c_y \end{split} \tag{1} \end{align} $$また、近似二次ベジェ曲線の\(a_x\)、\(b_x\)、\(c_x\)、\(a_y\)、\(b_y\)及び\(c_y\)を求める式は以下の通りです。
$$ \begin{align} |A|&=\sum{t^4}\sum{t^2}\sum{1}+2\sum{t^3}\sum{t^2}\sum{t}\\ &-\Bigl(\sum{t^2}\Bigr)^3-\Bigl(\sum{t^3}\Bigr)^2\sum{1}-\sum{t^4}\Bigl(\sum{t}\Bigr)^2 \end{align} \tag{2} $$ $$ \begin{align} a_x&=\frac{1}{|A|}\Bigl\lbrace\Bigl[\sum{t^2}\sum{1}-\Bigl(\sum{t}\Bigr)^2\Bigr]\sum{xt^2}\\ &\hspace{60px}+\Bigl[\sum{t^2}\sum{t}-\sum{t^3}\sum{1}\Bigr]\sum{xt}\\ &\hspace{75px}+\Bigl[\sum{t^3}\sum{t}-\Bigl(\sum{t^2}\Bigr)^2\Bigr]\sum{x}\Bigr\rbrace \end{align} \tag{3} $$ $$ \begin{align} b_x&=\frac{1}{|A|}\Bigl\lbrace\Bigl[\sum{t^2}\sum{t}-\sum{t^3}\sum{1}]\sum{xt^2}\\ &\hspace{60px}+\Bigl[\sum{t^4}\sum{1}-\Bigl(\sum{t^2}\Bigr)^2]\sum{xt}\\ &\hspace{75px}+\Bigl[\sum{t^3}\sum{t^2}-\sum{t^4}\sum{t}]\sum{x}\Bigr\rbrace \end{align} \tag{4} $$ $$ \begin{align} c_x&=\frac{1}{|A|}\Bigl\lbrace\Bigl[\sum{t^3}\sum{t}-\Bigl(\sum{t^2}\Bigr)^2]\sum{xt^2}\\ &\hspace{60px}+\Bigl[\sum{t^3}\sum{t^2}-\sum{t^4}\sum{t}]\sum{xt}\\ &\hspace{75px}+\Bigl[\sum{t^4}\sum{t^2}-\Bigl(\sum{t^3}\Bigr)^2]\sum{x}\Bigr\rbrace \end{align} \tag{5} $$ $$ \begin{align} a_y&=\frac{1}{|A|}\Bigl\lbrace\Bigl[\sum{t^2}\sum{1}-\Bigl(\sum{t}\Bigr)^2\Bigr]\sum{yt^2}\\ &\hspace{60px}+\Bigl[\sum{t^2}\sum{t}-\sum{t^3}\sum{1}\Bigr]\sum{yt}\\ &\hspace{75px}+\Bigl[\sum{t^3}\sum{t}-\Bigl(\sum{t^2}\Bigr)^2\Bigr]\sum{y}\Bigr\rbrace \end{align} \tag{6} $$ $$ \begin{align} b_y&=\frac{1}{|A|}\Bigl\lbrace\Bigl[\sum{t^2}\sum{t}-\sum{t^3}\sum{1}]\sum{yt^2}\\ &\hspace{60px}+\Bigl[\sum{t^4}\sum{1}-\Bigl(\sum{t^2}\Bigr)^2]\sum{yt}\\ &\hspace{75px}+\Bigl[\sum{t^3}\sum{t^2}-\sum{t^4}\sum{t}]\sum{y}\Bigr\rbrace \end{align} \tag{7} $$ $$ \begin{align} c_y&=\frac{1}{|A|}\Bigl\lbrace\Bigl[\sum{t^3}\sum{t}-\Bigl(\sum{t^2}\Bigr)^2]\sum{yt^2}\\ &\hspace{60px}+\Bigl[\sum{t^3}\sum{t^2}-\sum{t^4}\sum{t}]\sum{yt}\\ &\hspace{75px}+\Bigl[\sum{t^4}\sum{t^2}-\Bigl(\sum{t^3}\Bigr)^2]\sum{y}\Bigr\rbrace \end{align} \tag{8} $$step2
四つの近似二次ベジェ曲線それぞれの最接近点における\(t\)を求めます。二次ベジェ曲線と任意点\(P_t(x_t,y_t)\)の距離の二乗\(D\)は
$$ D=(a_xt^2+b_xt+c_x-x_t)^2+(a_yt^2+b_yt+c_y-y_t)^2 \tag{9} $$となります。よって、\(D^{\prime}=0\)の解が最接近点における\(t\)となります。
$$ \begin{align} &D^{\prime}=at^3+b^2+ct+d\\ &a=4(a_x^2+a_y^2)\\ &b=6(a_xb_x+a_yb_y)\\ &c=4a_x(c_x-x_t)+4a_y(c_y-y_t)+2(b_x^2+b_y^2)\\ &d=2b_x(c_x-x_t)+2b_y(c_y-y_t) \end{align} \tag{10} $$この方程式の解は以下に示すカルダノの公式によって求めます。
$$ \begin{align} &x_k=-\frac{b}{3a}+u_k+v_k \hspace{10px} (k=0,1,2)\\ &u_k=\omega^k\sqrt[3]{-q+\sqrt{q^2+p^3}}\\ &v_k=\omega^{3-k}\sqrt[3]{-q-\sqrt{q^2+p^3}}\\ &p=\frac{-b^2+3ac}{9a^2}, \hspace{10px} q=\frac{2b^3-9abc+27a^2d}{54a^3} \end{align} \tag{11} $$ただし、\(u,v\)は以下の式を満たす必要があります。
$$ uv=-p \tag{12} $$step3
複素数解とそれぞれの区間外解を除きます。例えば、\(0 \leq t \leq 0.25\)の範囲で求めた近似二次ベジェ曲線の解\(t_1\)は\(0 \leq t_1 \leq 0.25\)でない場合は除外します。残りの\(t\)から一番\(D\)が小さくなる\(t\)を探します。これにより、最接近点の近似点における\(t\)が求まります。
step4
step3で求めた\(t\)を初期値として、求根アルゴリズムを利用して三次ベジェ曲線における最接近点を求めます。今回はブレント法(Van Wijngaarden–Dekker–Brent Method)を用いました。
結果
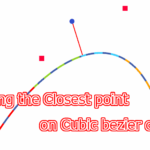
以上で説明した方法によって、Unity上で三次ベジェ曲線の最接近点を求めました。その結果は以下の通りです。赤い四角が三次ベジェ曲線のコントロールポイント、青い丸が任意点\(P_t\)、青い実線が三次ベジェ曲線、破線が各区間における近似二次ベジェ曲線、赤い実線が\(P_t\)と最接近点を結ぶ直線となっています。
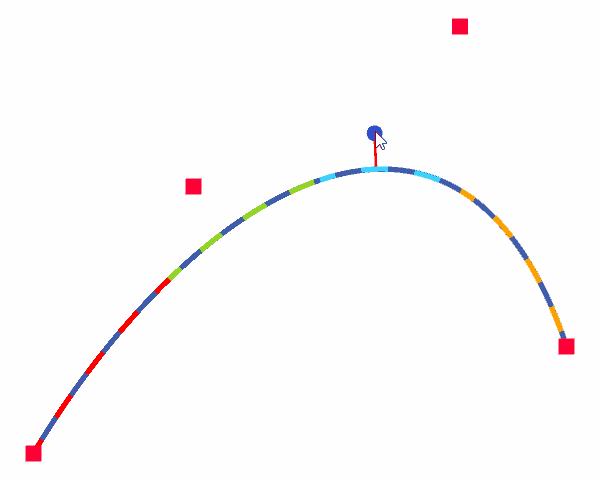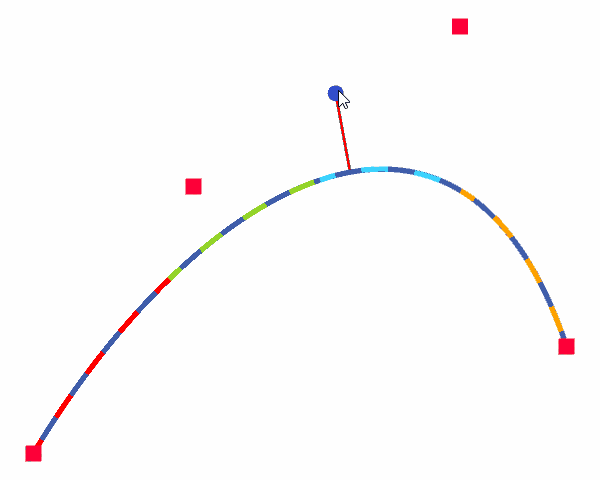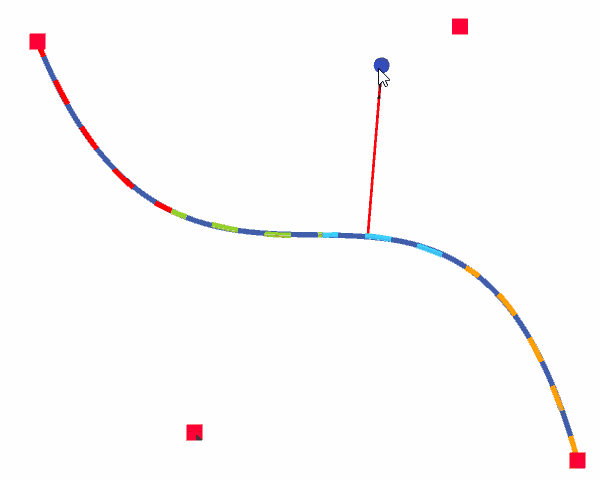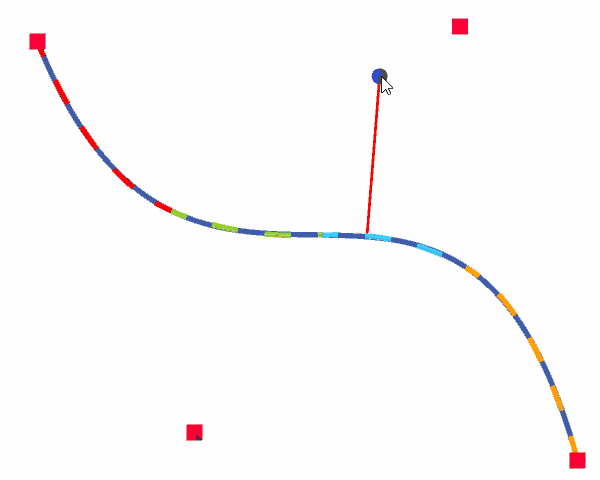
この結果より、最接近点が問題なく求められていることが分かります。また、ブレント法は3,4回の繰り返しで解へ収束しました。
参考文献
Numerical Recipes in Fortran 77, Second Edition:9.3 Van Wijngaarden–Dekker–Brent Method
-
前の記事
最小二乗法を用いた二次ベジェ曲線による三次ベジェ曲線の近似 2023.11.10
-
次の記事

ECS(Entity Component System) 基礎中の基礎 2025.01.09



コメントを書く