ベジェ曲線の最接近点
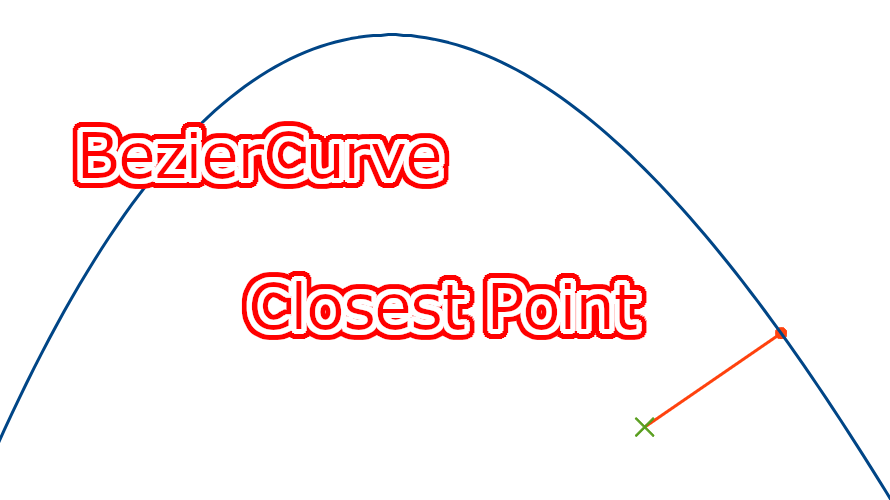
任意の座標からベジェ曲線上の最も近い点をニュートン法を用いて求めました。
ニュートン法
ニュートン法の方程式は
$$ x_{n+1} = x_n-\frac{f(x_n)}{f'(x_n)} $$です。これを繰り返し求めることで\(f(x) = 0\)となる\(x\)が求まります。しかし、条件によっては解に収束しないことがあります。
ベジェ曲線との距離
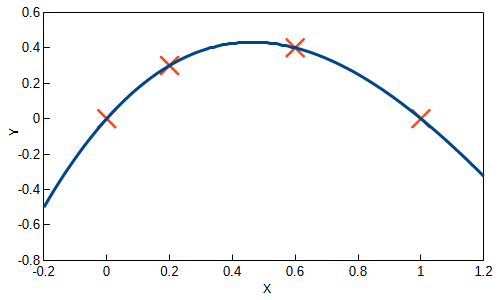
4点を通る三次ベジェ曲線で求めた式を用いてベジェ曲線を求めました。
$$ \begin{align} &P = (1-t)^3C_0 + 3(1 – t)^2tC_1 + 3(1 – t)t^2C_2 + t^3C_3 \tag{1}\\ &C_0 = P_0 \tag{2}\\ &C_3 = P_3 \tag{3}\\ &C_1 = \frac{(ag – ce)P_0 – gP_1 + cP_2 + (dg – ch)P_3}{cf – bg} \tag{4}\\ &C_2 = \frac{P_1 – aP_0 – dP_3 – bC_1}{c} \tag{5}\\ \end{align} $$使用した座標点は以下の通りです。
$$ \begin{align} &P_0(0, 0)\\ &P_1(0.2, 0.3),\ t_1=0.2\\ &P_2(0.6, 0.4),\ t_2=0.6\\ &P_3(1, 0)\\ \end{align} $$グラフに描画すると以下のようになります。
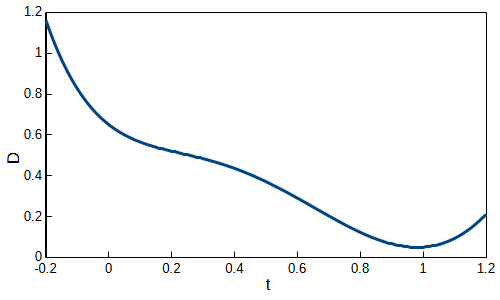
任意の点\(Q\)からベジェ曲線の距離dは
$$ d=\sqrt{(Q_x-P_x)^2+(Q_y-P_y)^2} \tag{6}\\ $$となります。\(d\)が最小となる\(t\)を求めると最接近点が分かります。つまり、\(d\)の微分値が0となる\(t\)を求めればよいということになります。ただ、平方根の計算はコストが高いので\(D=d^2\)を使用します。
$$ D=(Q_x-P_x)^2+(Q_y-P_y)^2 \tag{7}\\ $$最接近点を探す点を\(Q=(0.8, -0.1)\)とした場合、ベジェ曲線と点\(Q\)の距離の二乗\(D\)のグラフは以下のようになります。
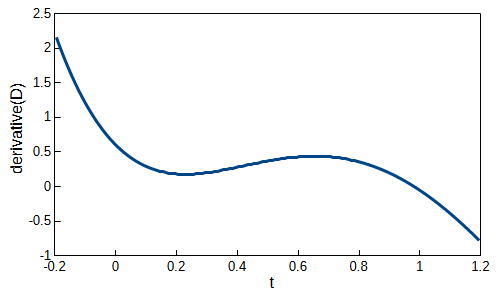
これを三点公式によって数値微分すると以下のグラフが得られます。ニュートン法は初期値によっては収束しない場合がありますが、このグラフより、点\(Q\)の\(x\)座標\(0.8\)をそのままニュートン法の初期値として使用すれば問題なく収束することが予想されます。
結果
ニュートン法によって解を求めた結果、最接近点の座標値は
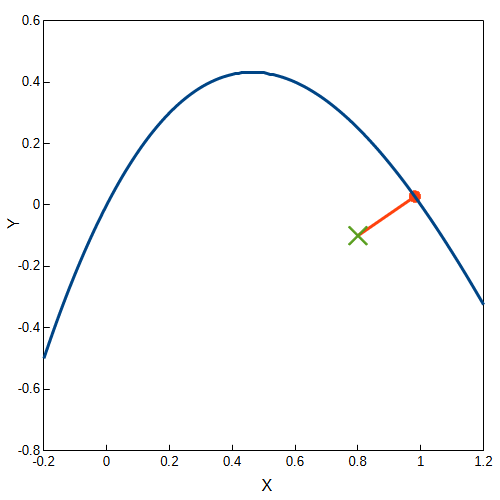
$$ x=0.981047,\ y=0.027298 $$と求まりました。この結果をグラフにすると以下のようになります。緑色の×が点\(Q\)、赤丸が求めた最接近点です。
参考サイト
-
前の記事
4点を通る三次ベジェ曲線 2023.04.30
-
次の記事
二次B-スプライン曲線の最接近点(式の展開) 2023.05.13
コメントを書く