PlayerとEnemyの衝突を検知し、Effectを再生します。 Script Component Player Playerの移動速度を決めるComponentです。 Playerがキー入力を受け取るためのComponentです。 以上のComponentを追加したEntityを作成します。 Enemy Enemyの名前と自身が破壊された際に再生するエフェクトをまとめたComponentです。 […]
キー入力(WASDキー)をInputSystemから取得してCubeを動かします。 Script Component Cubeの移動速度を決めるComponentです。 取得したキー入力を渡すためのComponentです。 以上のComponentを追加したEntityを作成します。 System ISystemはマネージドなフィールドを持つことができません。よって、InputSystemを利用す […]
ECS(Entity Component System) 基礎中の基礎で作成したCubeを大量に生成します。 Script Cube CubeDataで使用するデータを定義しています。 Entityの取得及びComponentの追加を行っています。 Cubeを動かすための処理です。今回は大量にCubeを動かすのでJobSytemを使用して並列に実行しています。 Cubeの生成 Prefabを使用し […]
原点回りにCubeが回転するだけの単純なサンプルです。 Script CubeDataで使用するデータを定義します。 CubeAuthoringではEntityを取得し、そのEntityにCubeData Componentを追加しています。よって、CubeAuthoringにはCubeを動かすための処理はありません。また、GetEntityでTransformUsageFlags.Dynami […]
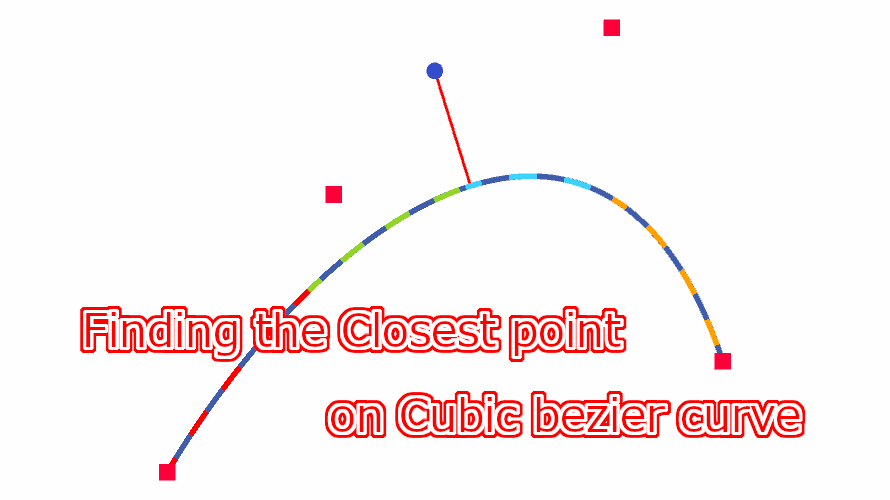
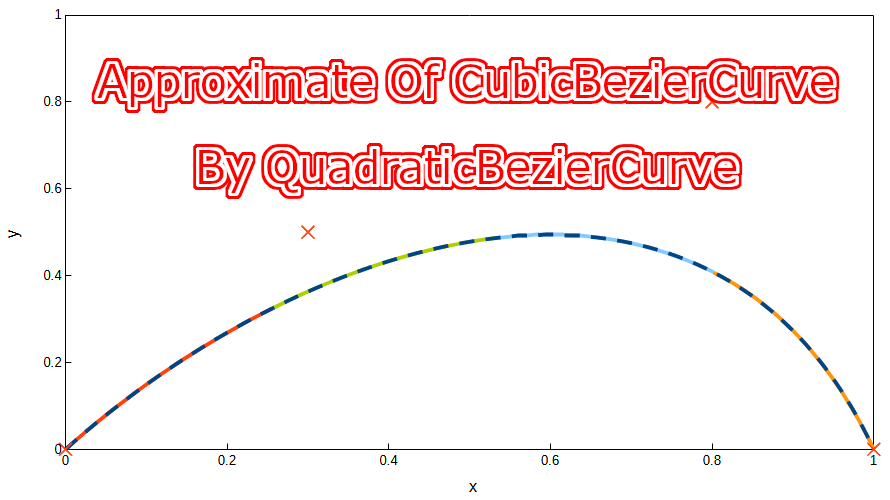
三次ベジェ曲線の最接近点 最小二乗法を用いた二次ベジェ曲線による三次ベジェ曲線の近似によって求めた四つの近似二次ベジェ曲線における最接近点を求め、その結果から三次ベジェ曲線における最接近点を求めます。 step1 最小二乗法を用いた二次ベジェ曲線による三次ベジェ曲線の近似を用いて四つに区切った三次ベジェ曲線において、それぞれの区間に対し近似二次ベジェ曲線を求めます。二次ベジェ曲線は以下の通りで […]
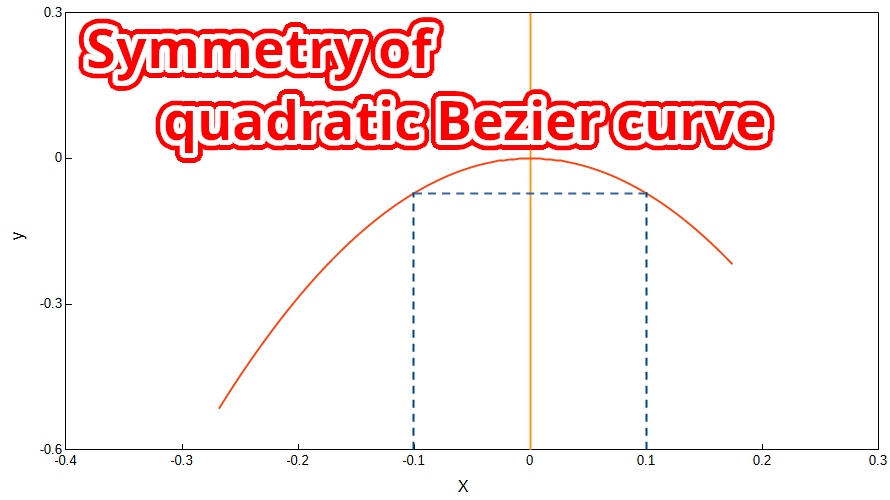
二次ベジェ曲線の式 二次ベジェ曲線の式を以下の通りです。 $$ \begin{align} \begin{split} &x(t)=a_xt^2+b_xt+c_x\\ &y(t)=a_yt^2+b_yt+c_y \end{split} \tag{1} \end{align} $$ $$ \begin{align} \begin{split} &a_x=(P_{0x} […]
二次ベジェ曲線 二次ベジェ曲線の式は以下の通りです。 $$ B(t)=(1-t)^2P_0+2(1-t)tP_1+t^2P_2 \tag{1} $$ よって、\(x\)、\(y\)はそれぞれ $$ \begin{split} \begin{align} &x(t)=(1-t)^2P_{0x}+2(1-t)tP_{1x}+t^2P_{2x}\\ &y(t)=(1-t)^2P_{ […]
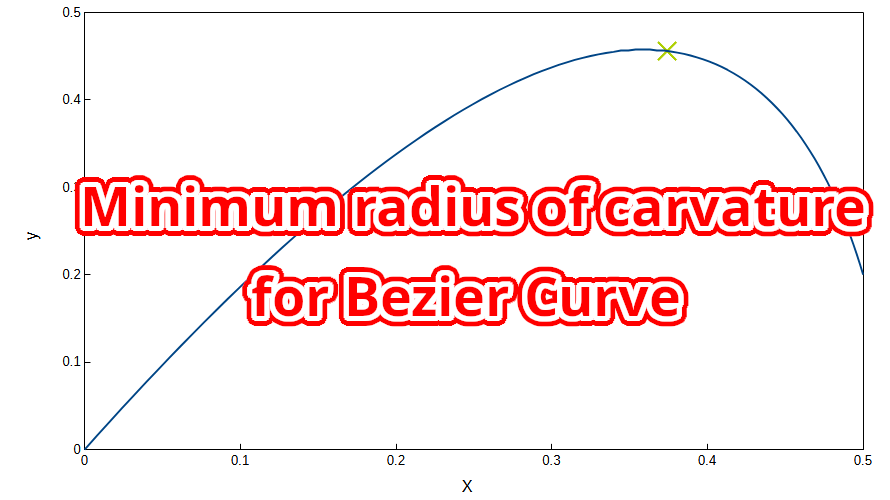
二次ベジェ曲線の微分 二次ベジェ曲線の式は以下の通りです。 $$ B(t)=(1-t)^2P_0+2(1-t)tP_1+t^2P_2 \tag{1} $$ よって、\(x\)、\(y\)はそれぞれ $$ \begin{align} &x(t)=(1-t)^2P_{0x}+2(1-t)tP_{1x}+t^2P_{2x} \tag{2}\\ &y(t)=(1-t)^2P_{0y} […]
一次導関数 n次B-スプライン曲線 n次B-スプライン曲線の式を以下に示します。mはノットベクトルの数です。 $$ \begin{align} \begin{split} &S(u)=\sum_{j=0}^{m-n-2}P_jb_{j,n}(u)\\\\ &b_{j,0}(u):=\begin{cases} 1 \hspace{10pt} if \hspace{10pt} u_ […]
前回求めた式を利用して制御点が5点の場合における二次B-スプライン曲線の最接近点を求めます。 式の導出 前回求めた二次B-スプライン曲線の式は $$ \begin{align} S&(u)=au^2+bu+c \tag{1}\\\\ a&=9b_{2,0}P_0+(9b_{1,0}-\frac{27}{2}b_{2,0}+\frac{9}{2}b_{3,0})P_1\\\\ […]