シェーダでノイズ1
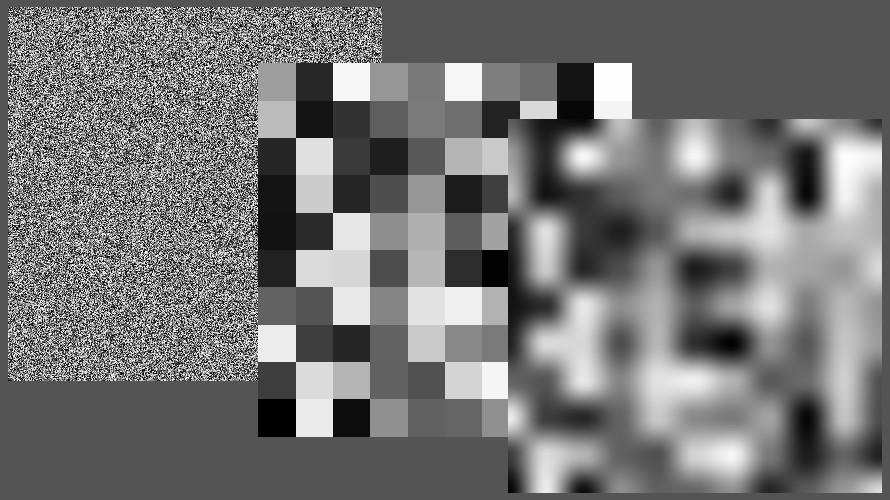
二次元ランダムノイズ
不規則な値を返す関数によってテクセルごとの色を決定します。ただし、使用する関数は入力した値に応じて決まった値を返す疑似ランダム関数を使用しています。
シェーダ
ramdom関数へuv座標を渡すことで不規則な値を得ています。この値を色として出力しています。Seedの値を変更すると異なる結果が得られます。Seedをfloatにすると、値によっては常に0となるようです。そのため、Seedはintにしています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
Shader "Noise/Random" { Properties { _MainTex ("Texture", 2D) = "white" {} _Seed ("Seed", Int) = 0 } SubShader { Tags { "RenderType"="Opaque" } Pass { CGPROGRAM #pragma vertex vert #pragma fragment frag #include "UnityCG.cginc" struct appdata { float4 vertex : POSITION; float2 uv : TEXCOORD0; }; struct v2f { float2 uv : TEXCOORD0; UNITY_FOG_COORDS(1) float4 vertex : SV_POSITION; }; sampler2D _MainTex; float4 _MainTex_ST; int _Seed; float random(float2 st, int seed) { return frac(sin(dot(st.xy, float2(12.9898, 78.233)) + seed) * 43758.5453123); } v2f vert (appdata v) { v2f o; o.vertex = UnityObjectToClipPos(v.vertex); o.uv = TRANSFORM_TEX(v.uv, _MainTex); return o; } fixed4 frag (v2f i) : SV_Target { fixed4 col; col.rgb = random(i.uv, _Seed); col.a = 1; return col; } ENDCG } } } |
実行結果
上記シェーダの実行結果は以下の通りです。これより、不規則な値が得られていることがわかります。
ブロックノイズ
座標を格子状に区切り、各格子ごとに代表となる値を選んだ後に、その値で格子全体を塗りつぶします。
計算方法
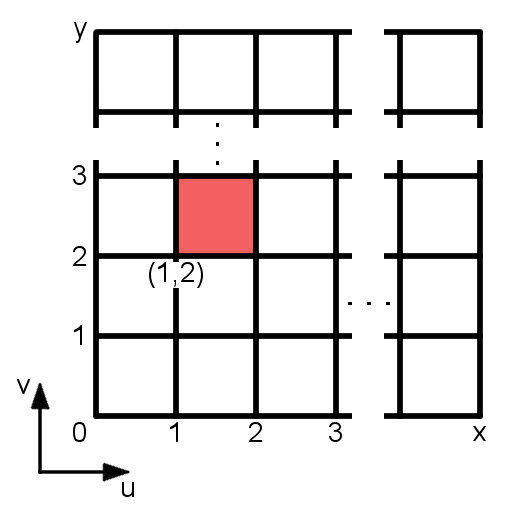
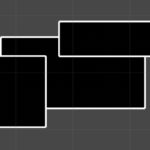
始めにuv座標に定数を掛けます。その値の小数点を切り捨て、整数を求めます。この整数を使用してランダムな値を得ます。ただし、ランダムな値は整数が変わらなければ、常に同じ値を返します。そのため、整数が同じになる領域は常に同じ値が得られます。例えば、\(x\)が\(1\leq x \lt2\)で \(y\)が\(2\leq y \lt3\)の範囲においては、整数は常に\((1,2)\)となります。つまり、下図の赤い範囲では\((1,2)\)をもとに求められた値となります。そのため、各格子内は同じ値で塗りつぶされます。
shader
uv座標にかけた値(_Size)が格子数となります。また、代表となる値は 、uv座標に格子数を掛けた値(st)の小数点を切り捨てた値(ipos)を使用しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 |
Shader "Noise/BlockNoise" { Properties { _MainTex ("Texture", 2D) = "white" {} _Seed ("Seed", Int) = 0 _Size ("Size", Int) = 1 } SubShader { Tags { "RenderType"="Opaque" } Pass { CGPROGRAM #pragma vertex vert #pragma fragment frag #include "UnityCG.cginc" struct appdata { float4 vertex : POSITION; float2 uv : TEXCOORD0; }; struct v2f { float2 uv : TEXCOORD0; float4 vertex : SV_POSITION; }; sampler2D _MainTex; float4 _MainTex_ST; int _Seed; int _Size; float random(float2 st, int seed) { return frac(sin(dot(st.xy, float2(12.9898, 78.233)) + seed) * 43758.5453123); } v2f vert (appdata v) { v2f o; o.vertex = UnityObjectToClipPos(v.vertex); o.uv = TRANSFORM_TEX(v.uv, _MainTex); return o; } fixed4 frag (v2f i) : SV_Target { fixed4 col; float2 st = i.uv * max(_Size, 1); float2 ipos = floor(st); col.rgb = random(ipos, _Seed); col.a = 1; return col; } ENDCG } } } |
実行結果
実行結果は以下の通りです。先ほどのランダムノイズを拡大したような結果が得られます。
Sizeを大きくするとランダムノイズのようになります。
バリューノイズ
先ほどのブロックノイズをぼかしたような結果が得られるノイズです。このノイズでは格子の四隅(格子点)で得られるランダムな値を格子点までの距離に応じて補間し、値を決定します。
計算方法
下の図は任意の格子を示しています。点mの値を点aと点bの値を補間することにより求めます。同様に、点nの値を点cと点dの値を補間することにより求めます。 そして、点mの値と点nの値を補間することで、点Pにおける値が求まります。バリューノイズで使用する補間方法は線形補間ではなくエルミート補間を使用します。これにより、ノイズが滑らかに変化します。
点aから点Pのu方向への距離は\(frac(p_{u})\)となります。同様に点cと点Pの
u方向への距離は\(frac(p_{u})\)となります。 また、点mから点Pのv方向への距離は\(frac(p_{v})\)となります。これより、点mと点nの値は
shader
noise()でバリューノイズを計算しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
Shader "Noise/ValueNoise" { Properties { _MainTex ("Texture", 2D) = "white" {} _Seed ("Seed", Int) = 0 _Size ("Size", Int) = 1 } SubShader { Tags { "RenderType"="Opaque" } LOD 100 Pass { CGPROGRAM #pragma vertex vert #pragma fragment frag #include "UnityCG.cginc" struct appdata { float4 vertex : POSITION; float2 uv : TEXCOORD0; }; struct v2f { float2 uv : TEXCOORD0; float4 vertex : SV_POSITION; }; sampler2D _MainTex; float4 _MainTex_ST; int _Seed; int _Size; float rand(float2 st, int seed) { return frac(sin(dot(st.xy, float2(12.9898, 78.233)) + seed) * 43758.5453123); } float noise(float2 st, int seed) { float2 ip = floor(st); float2 f = frac(st); float a = rand(ip, seed); float b = rand(ip + float2(1, 0), seed); float c = rand(ip + float2(0, 1), seed); float d = rand(ip + float2(1, 1), seed); float2 t = f * f * (3 - 2 * f); return lerp(a, b, t.x) + (c - a) * t.y * (1 - t.x) + (d - b) * t.x * t.y; //return lerp(lerp(a, b, t.x), lerp(c, d, t.x), t.y); } v2f vert (appdata v) { v2f o; o.vertex = UnityObjectToClipPos(v.vertex); o.uv = TRANSFORM_TEX(v.uv, _MainTex); return o; } fixed4 frag (v2f i) : SV_Target { fixed4 col; col.rgb = noise(i.uv * _Size, _Seed); col.a = 1; return col; } ENDCG } } } |
noise()の戻り値が
|
1 |
return lerp(a, b, t.x) + (c - a) * t.y * (1 - t.x) + (d - b) * t.x * t.y; |
となっていますが、これは
$$ \begin{align} &lerp[lerp\{a,b,t_{x}\},lerp\{c,d,t_{x}\},t_{y}]\\ & \ =lerp\{bt_{x}-a(1-t_{x}),dt_{x}-c(1-t_{x}),t_{y}\}\\ & \ =\{dt_{x}-c(1-t_{x})\}t_{y}+\{bt_{x}-a(1-t_{x})\}(1-t_{y})\\ & \ =(d-b)t_{x}t_{y}+(c-a)(1-t_{x})t_{y}+bx+a(1-t{x})\\ & \ =(d-b)t_{x}t_{y}+(c-a)(1-t_{x})t_{y}+lerp(a,b,t_{x}) \end{align} $$と求められた式であるので、戻り値を
|
1 |
return lerp(lerp(a, b, t.x), lerp(c, d, t.x), t.y); |
と変更しても同じ結果が得られます。
実行結果
上記shaderを実行した結果は以下の通りです。ブロックノイズをぼかしたような結果が得られます。
参考サイト
-
前の記事

UI要素をScriptから作成 2019.01.23
-
次の記事
RectTransformについてのメモ 2019.02.03

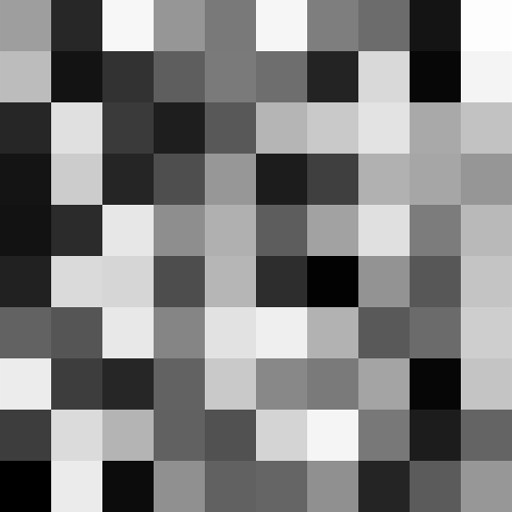









コメントを書く