二次ベジェ曲線の対称性

2023.07.28
Math
ベジェ曲線

1. 二次ベジェ曲線
2. ベジェ曲線の回転
- 2.1. 曲率半径が最小となる座標における法線
3. 対称性の確認

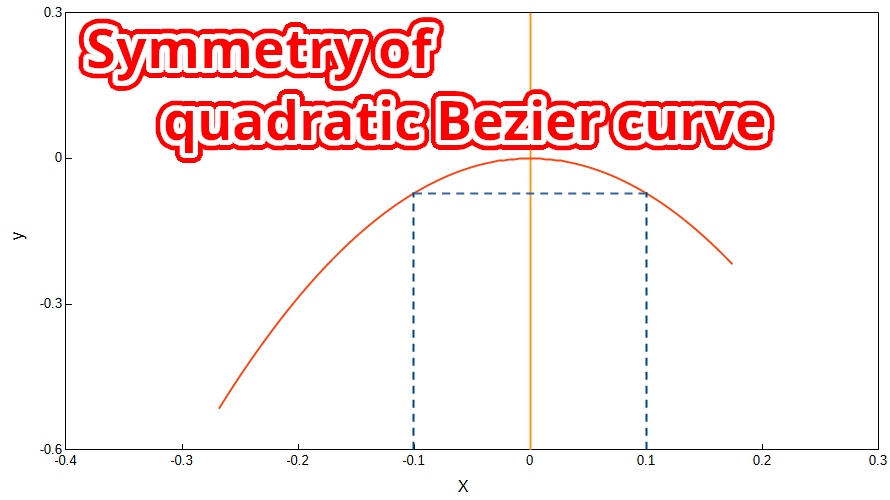
二次ベジェ曲線

　二次ベジェ曲線の式は以下の通りです。

$$ B(t)=(1-t)^2P_0+2(1-t)tP_1+t^2P_2 \tag{1} $$

よって、$x$、$y$はそれぞれ

$$ \begin{split} \begin{align} &x(t)=(1-t)^2P_{0x}+2(1-t)tP_{1x}+t^2P_{2x}\\ &y(t)=(1-t)^2P_{0y}+2(1-t)tP_{1y}+t^2P_{2y} \end{align} \end{split} \tag{2} $$

式$(2)$を整理すると、以下の式となります。

$$ \begin{split} \begin{align} &x(t)=\frac{1}{2}a_xt^2+b_xt+c_x\\ &a_x=2(P_{0x}-2P_{1x}+P_{2x})\\ &b_x=2(-P_{0x}+P_{1x})\\ &c_x=P_{0x}\\ \end{align} \end{split} \tag{3} $$ $$ \begin{split} \begin{align} &y(t)=\frac{1}{2}a_yt^2+b_yt+c_y\\ &a_y=2(P_{0y}-2P_{1y}+P_{2y})\\ &b_y=2(-P_{0y}+P_{1y})\\ &c_y=P_{0y} \end{align} \end{split} \tag{4} $$

ベジェ曲線の回転

　二次元座標において座標$(x,y)$を原点回りに$θ$回転させた座標$X,Y$は以下の通りです。

$$ \begin{split} \begin{align} &X=xcosθ-ysinθ\\ &Y=xsinθ+ycosθ \end{align} \end{split} \tag{5} $$

曲率半径が最小となる座標における法線

　ベジェ曲線において曲率半径が最小となる変数$t$は前回の記事（二次ベジェ曲線における曲率半径の極小値）より

$$ t_r=-\frac{a_xb_x+a_yb_y}{a_x^2+a_y^2} \tag{6} $$

であるので、曲率半径が最小となる点における接線の傾き$a_t$は以下の通りです。

$$ a_t=\frac{dy}{dx}=\frac{a_yt+b_y}{a_xt+b_x} \tag{7} $$

式$(7)$へ式$(6)$を代入し整理すると$a_t$は

$$ a_t=\frac{a_x(a_xb_y-a_yb_x)}{a_y(a_yb_x-a_xb_y)} \tag{8} $$

と求まります。よって、曲率半径が最小となる点における法線の傾き$a_n$は

$$ a_n=-\frac{a_y(a_yb_x-a_xb_y)}{a_x(a_xb_y-a_yb_x)} \tag{9} $$

となります。これより、曲率半径が最小となる点における法線ベクトル$\vec{n}$は

$$ \vec{n}=\left( 1, \space -\frac{a_y(a_yb_x-a_xb_y)}{a_x(a_xb_y-a_yb_x)} \right) \tag{10} $$

であり、正規化すると

$$ \frac{\vec{n}}{|\vec{n}|}=\left(\frac{1}{\sqrt{1+n_y^2}}, \space \frac{n_y}{\sqrt{1+n_y^2}} \right) \tag{11} $$

となります。よって、$y$軸と$\vec{n}$がなす角度を$θ$とすると$cosθ$と$sinθ$は以下のようになります。

$$ \begin{align} &cosθ=\frac{n_y}{\sqrt{1+n_y^2}}, \space sinθ=\frac{1}{\sqrt{1+n_y^2}}\\ \tag{12} &n_y=-\frac{a_y(a_yb_x-a_xb_y)}{a_x(a_xb_y-a_yb_x)} \end{align} $$

対称性の確認

　二次ベジェ曲線の曲率半径の極小値における点$(x_r, y_r)$は

$$ \begin{split} \begin{align} &x_r=\frac{1}{2}a_xt_r^2+b_xt_r+c_x\\ &y_r=\frac{1}{2}a_yt_r^2+b_yt_r+c_y\\ \end{align} \end{split} \tag{13} $$

です。$t=t_r-t_s$及び$t=t_r+t_s$としたときの座標$(x_1,y_1)$と$(x_2, y_2)$は式$(2)$より

$$ \begin{split} \begin{align} &x_1=\frac{1}{2}a_x(t_r^2-2t_rt_s+t_s^2)+b_x(t_r-t_s)+c_x\\ &y_1=\frac{1}{2}a_y(t_r^2-2t_rt_s+t_s^2)+b_y(t_r-t_s)+c_y\\ &x_2=\frac{1}{2}a_x(t_r^2+2t_rt_s+t_s^2)+b_x(t_r+t_s)+c_x\\ &y_2=\frac{1}{2}a_y(t_r^2+2t_rt_s+t_s^2)+b_y(t_r+t_s)+c_y\\ \end{align} \end{split} \tag{14} $$

となります。この座標を式$(13)$によって移動した座標は以下の通りになります。

$$ \begin{split} \begin{align} &x_1=\frac{1}{2}a_x(-2t_rt_s+t_s^2)-b_xt_s\\ &y_1=\frac{1}{2}a_y(-2t_rt_s+t_s^2)-b_yt_s\\ &x_2=\frac{1}{2}a_x(2t_rt_s+t_s^2)+b_xt_s\\ &y_2=\frac{1}{2}a_y(2t_rt_s+t_s^2)+b_yt_s\\ \end{align} \end{split} \tag{15} $$

y座標

　式$(5)$と式$(15)$より回転後のy座標$Y_1$と$Y_2$は

$$ \begin{split} \begin{align} Y_1&=x_1sinθ+y_1cosθ\\ &=\frac{1}{2}t_s^2(a_xsinθ+a_ycosθ)-t_s(a_xt_r+b_x) sinθ-t_s(a_yt_r+b_y) cosθ\\ Y_2&=x_2sinθ+y_2cosθ\\ &=\frac{1}{2}t_s^2(a_xsinθ+a_ycosθ)+t_s(a_xt_r+b_x) sinθ+t_s(a_yt_r+b_y) cosθ\\ \end{align} \end{split} \tag{16} $$

となります。ここで

$$ \begin{split} \begin{align} (a_xt_r+b_x)sinθ&=\left(-\frac{a_x^2b_x+a_xa_yb_y}{a_x^2+a_y^2}+b_x \right)\cdot\frac{1}{\sqrt{1+n_y^2}}\\ &=\left( \frac{a_y^2b_x-a_xa_yb_y}{a_x^2+a_y^2} \right)\cdot\frac{1}{1+n_y^2}\\ (a_yt_r+b_y)cosθ&=\left(-\frac{a_xa_yb_y+a_y^2b_x}{a_x^2+a_y^2}+b_y \right)\cdot\frac{n_y}{\sqrt{1+n_y^2}}\\ &=\left(-\frac{a_y^2b_x-a_xa_yb_y}{a_x^2+a_y^2} \right)\cdot\frac{1}{1+n_y^2} \end{align} \end{split} \tag{17} $$

であるので、$Y_1$と$Y_2$は

$$ \begin{split} \begin{align} Y_1&=\frac{1}{2}t_s^2(a_xsinθ+a_ycosθ)\\ Y_2&=\frac{1}{2}t_s^2(a_xsinθ+a_ycosθ)\\ \end{align} \end{split} \tag{18} $$

となり、$t=t_r-t_s$と$t=t_r+t_s$において$Y_1=Y_2$であることが分かりました。

x座標

　式$(5)$と式$(15)$より回転後のx座標$X_1$と$X_2$は

$$ \begin{split} \begin{align} X_1&=x_1cosθ-y_1sinθ\\ &=\frac{1}{2}t_s^2(a_xcosθ-a_ysinθ)-t_s(a_xt_r+b_x) cosθ+t_s(a_yt_r+b_y) sinθ\\ X_2&=x_2cosθ-y_2sinθ\\ &=\frac{1}{2}t_s^2(a_xcosθ-a_ysinθ)+t_s(a_xt_r+b_x) cosθ-t_s(a_yt_r+b_y) sinθ\\ \end{align} \end{split} \tag{19} $$

となります。ここで

$$ \begin{split} \begin{align} a_xcosθ-a_ysinθ&=a_x\frac{n_y}{\sqrt{1+n_y^2}}-a_y\frac{1}{\sqrt{1+n_y^2}}\\ &=(a_xn_y+a_y)\frac{1}{\sqrt{1+n_y^2}}\\ &=0 \end{align} \end{split} \tag{20} $$

であるので、$X_1$と$X_2$は

$$ \begin{split} \begin{align} &X_1=-t_s(a_xt_r+b_x)cosθ+t_s(a_tt_r+b_y) sinθ\\ &X_2=t_s(a_xt_r+b_x)cosθ-t_s(a_tt_r+b_y) sinθ\\ \end{align} \end{split} \tag{21} $$

となり、$t=t_r-t_s$と$t=t_r+t_s$のにおいて$X_1=-X_2$であることが分かりました。