二次ベジェ曲線における曲率半径の極小値

2023.07.26
Math
ベジェ曲線

1. 二次ベジェ曲線の微分
2. 曲率半径
3. 曲率半径の極小値
4. グラフ
5. 備考

二次ベジェ曲線の微分

　二次ベジェ曲線の式は以下の通りです。

$$ B(t)=(1-t)^2P_0+2(1-t)tP_1+t^2P_2 \tag{1} $$

よって、$x$、$y$はそれぞれ

$$ \begin{align} &x(t)=(1-t)^2P_{0x}+2(1-t)tP_{1x}+t^2P_{2x} \tag{2}\\ &y(t)=(1-t)^2P_{0y}+2(1-t)tP_{1y}+t^2P_{2y} \tag{3} \end{align} $$

となります。これより、$x(t)$の一階導関数と二階導関数は以下の式となります。

$$ \begin{align} \begin{split} &x^{\prime}(t)=a_xt+b_x\\ &x^{\prime\prime}(t)=a_x\\ &a_x=2(P_{0x}-2P_{1x}+P_{2x})\\ &b_x=2(-P_{0x}+P_{1x})\\ \end{split} \tag{4} \end{align} $$

また、$y(t)$の一階導関数と二階導関数は以下の式となります。

$$ \begin{align} \begin{split} &y^{\prime}(t)=a_yt+b_y\\ &y^{\prime\prime}(t)=a_y\\ &a_y=2(P_{0y}-2P_{1y}+P_{2y})\\ &b_y=2(-P_{0y}+P_{1y}) \end{split} \tag{5} \end{align} $$

曲率半径

　ベジェ曲線を$y=B(x)$とすると、曲率半径は以下の式となります。

$$ R=\frac{(1+B^{\prime}(x)^2)^\frac{3}{2}}{{\lvert B^{\prime\prime}(x)}\rvert} \tag{6} $$

曲率半径の極小値

　曲率半径の極小値を求めるために、曲率半径$R$の一階導関数$R’$を求めます。$R’$は

$$ R^{\prime}=\frac{3(1+B^{\prime}(x)^2)^\frac{1}{2}B^{\prime}(x)B^{\prime\prime}(x)\lvert B^{\prime\prime}(x)\rvert -(1+B^{\prime}(x)^2)^\frac{3}{2}\lvert B^{\prime\prime}(x)\rvert^{\prime}} {B^{\prime\prime}(x)^2} \tag{7} $$

となります。$R’=0$となる$t$を求めます。式$(7)$より

$$ \begin{align} \frac{3(1+B^{\prime}(x)^2)^\frac{1}{2}B^{\prime}(x)B^{\prime\prime}(x)\lvert B^{\prime\prime}(x)\rvert -(1+B^{\prime}(x)^2)^\frac{3}{2}\lvert B^{\prime\prime}(x)\rvert^{\prime}} {B^{\prime\prime}(x)^2}=0 \tag{8} \end{align} $$

$\lvert B^{\prime\prime}(x) \rvert$は

$$ \lvert B^{\prime\prime}(x) \rvert= \begin{cases} B^{\prime\prime}(x)\space (B^{\prime\prime}(x)\geq0)\\ -B^{\prime\prime}(x)\space (B^{\prime\prime}(x)<0)\\ \end{cases} \tag{9} $$

であり、$\lvert B^{\prime\prime}(x) \rvert^\prime$は

$$ \lvert B^{\prime\prime}(x) \rvert^\prime= \begin{cases} B^{\prime\prime\prime}(x)\space (B^{\prime\prime}(x)\geq0)\\ -B^{\prime\prime\prime}(x)\space (B^{\prime\prime}(x)<0)\\ \end{cases} \tag{10} $$

であるので、$式(8)$は

$$ \frac{3(1+B^{\prime}(x)^2)^\frac{1}{2}B^{\prime}(x)B^{\prime\prime}(x)^2 -(1+B^{\prime}(x)^2)^\frac{3}{2}B^{\prime\prime\prime}(x)} {B^{\prime\prime}(x)^2}=0 \tag{11} $$

となります。上式より

$$ 1+B^{\prime}(x)^2=0\\ \tag{12} $$

であるとき、$R’=0$となることがわかります。この式より解を求めます。$B^{\prime}(x)$は

$$ B^{\prime}(x)=\frac{x^{\prime}(t)}{y^{\prime}(t)}=\frac{a_yt+b_y}{a_xt+b_x} \tag{13} $$

なので式$(12)$は

$$ 1+B^{\prime}(x)^2=1+\left( \frac{a_yt+b_y}{a_xt+b_x} \right)^2\\ \tag{14} $$

となります。この式を整理すると

$$ (a_x^2+a_y^2)t^2+2(a_xb_x+a_yb_y)t+b_x^2+by^2=0 \tag{15} $$

となります。よって、式$(15)$の解は

$$ t=\frac{-2(a_xb_x+a_yb_y)\pm\sqrt{4(a_xb_x+a_yb_y)^2-4(a_x^2+a_y^2)(b_x^2+by^2)}}{2(a_x^2+a_y^2)} \tag{16} $$

と求まります。次に、式$(11)$を整理して他の解を求めます。$B^{\prime\prime}(x)$及び$B^{\prime\prime\prime}(x)$は以下の通りです。

$$ B^{\prime\prime}(x)=\frac{x^{\prime}(t)y^{\prime\prime}(t)-x^{\prime\prime}(t)y^{\prime}(t)}{x^{\prime}(t)^3} \tag{17} $$ $$ \begin{align} B^{\prime\prime\prime}(x)=-3B^{\prime\prime}(x)\frac{x^{\prime\prime}(t)}{x^{\prime}(t)^2} \tag{18} \end{align} $$

式$(17)$と式$(18)$を用いると式$(11)$は

$$ y^{\prime}(t)y^{\prime\prime}(t)+x^{\prime}(t)x^{\prime\prime}(t)=0 \tag{19} $$

上式に式$(4)$及び式$(5)$に代入し整理すると

$$ t=-\frac{a_xb_x+a_yb_y}{a_x^2+a_y^2} \tag{20} $$

となります。解は式$(16)$及び式$(20)$と求まりました。二次ベジェ曲線の曲率半径の極値は一つなので

$$ t=-\frac{a_xb_x+a_yb_y}{a_x^2+a_y^2} $$

と一意に求まります。

グラフ

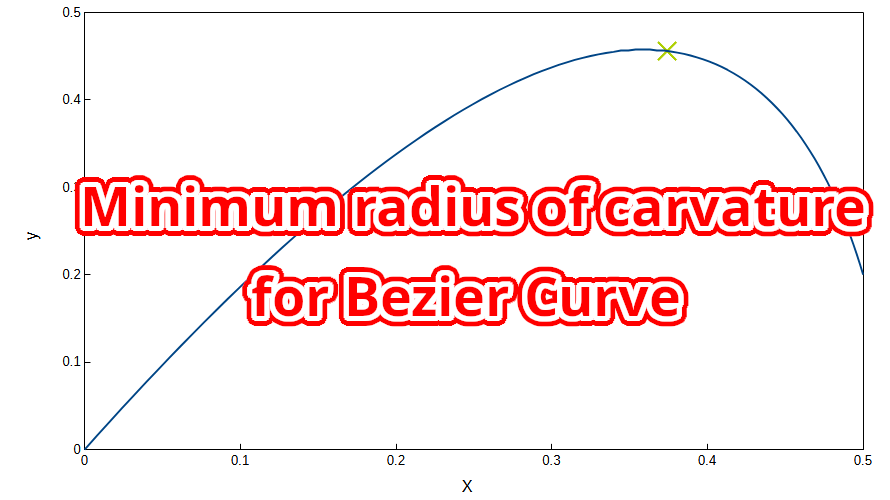
以下の条件で曲率半径が極小値になる変数$t$を求めました。

$$ P_0(0,0),\space P_1(0.4,0.8),\space P_2(0.5,0.2) $$

式$(20)$より変数変数$t$は

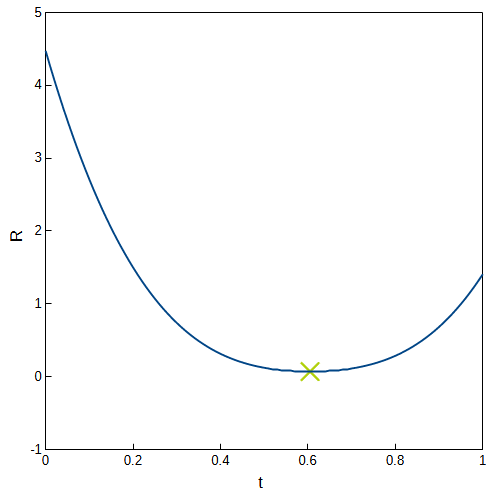
$$ t=0.6048780… $$

となります。これより、曲率半径のグラフを描画すると以下のようになります。緑色の×が曲率半径の最小値です。

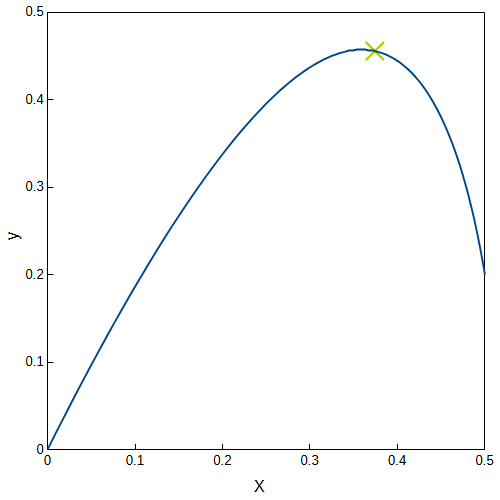
また、座標を計算しグラフへ描画すると以下のようになります。

備考

媒介変数表示された関数の二階微分

$$ \begin{align} \frac{d^2y}{dx^2}&=\frac{d}{dx}\left(\frac{dy}{dx}\right)\\ &=\frac{d}{dt}\left(\frac{dy}{dx}\right)\cdot\frac{dt}{dx}\\ &=\frac{d}{dt}\left(\frac{\frac{dy}{dt}}{\frac{dx}{dt}}\right)\cdot\frac{dt}{dx}\\ &=\frac{\frac{d^2y}{dt^2}\cdot\frac{dx}{dt}-\frac{dy}{dt}\cdot\frac{d^2x}{dt^2}}{(\frac{dx}{dt})^2}\cdot\frac{dt}{dx}\\ &=\frac{\frac{d^2y}{dt^2}\cdot\frac{dx}{dt}-\frac{dy}{dt}\cdot\frac{d^2x}{dt^2}}{(\frac{dx}{dt})^3}\\ \end{align} $$

媒介変数表示された関数の三階微分

$$ \begin{align} \frac{d^3y}{dx^3}&=\frac{d}{dx}\left(\frac{d^2y}{dx^2} \right)\\ &=\frac{d}{dt}\left(\frac{d^2y}{dx^2} \right)\cdot\frac{dt}{dx}\\ &=\frac{d}{dt}\left(\frac{\frac{d^2y}{dt^2}\cdot\frac{dx}{dt}-\frac{dy}{dt}\cdot\frac{d^2x}{dt^2}}{(\frac{dx}{dt})^3} \right)\cdot\frac{dt}{dx}\\ &=\frac{\left(\frac{d^3y}{dt^3}\cdot\frac{dx}{dt}-\frac{dy}{dt}\cdot\frac{d^3x}{dt^3}\right)\cdot\frac{dx}{dt} -3\left(\frac{d^2y}{dt^2}\cdot\frac{dx}{dt}-\frac{dy}{dt}\cdot\frac{d^2x}{dt^2}\right)\cdot\frac{d^2x}{dt^2}} {\left( \frac{dx}{dt}\right)^5} \end{align} $$

式$(18)$の導出

$$ B^{\prime\prime\prime}(x)=\frac {\lbrace x^{\prime}(t)y^{\prime\prime\prime}(t)-x^{\prime\prime\prime}(t)y^{\prime}(t)\rbrace x^{\prime}(t) -3\lbrace x^{\prime}(t)y^{\prime\prime}(t)-x^{\prime\prime}(t)y^{\prime}(t)\rbrace x^{\prime\prime}(t)} {x^{\prime}(t)^7} $$

$x(t)$及び$y(t)$は二次式であることから、$x^{\prime\prime\prime}(t)=0$及び$y^{\prime\prime\prime}(t)=0$となるので

$$ \begin{align} B^{\prime\prime\prime}(x)&=\frac {-3\lbrace x^{\prime}(t)y^{\prime\prime}(t)-x^{\prime\prime}(t)y^{\prime}(t)\rbrace x^{\prime\prime}(t)} {x^{\prime}(t)^5}\\ &=-3\frac{ x^{\prime}(t)y^{\prime\prime}(t)-x^{\prime\prime}(t)y^{\prime}(t) }{x^{\prime}(t)^3} \cdot \frac{x^{\prime\prime}(t)}{x^{\prime}(t)^2}\\ &=-3B^{\prime\prime}(x)\frac{x^{\prime\prime}(t)}{x^{\prime}(t)^2} \end{align} $$

式$(19)$の導出

$$ \begin{align} 3(1+B^{\prime}(x)^2)^\frac{1}{2}B^{\prime}(x)+ \frac{3(1+B^{\prime}(x)^2)^\frac{3}{2}\frac{x^{\prime\prime}(t)}{x^{\prime}(t)^2}} {B^{\prime\prime}(x)}=0 \end{align} $$ $$ B^{\prime}(x)B^{\prime\prime}(x)+ (1+B^{\prime}(x)^2)\frac{x^{\prime\prime}(t)}{x^{\prime}(t)^2}=0 $$ $$ \frac{y^{\prime}(t)}{x^{\prime}(t)}\cdot\frac{x^{\prime}(t)y^{\prime\prime}(t)-x^{\prime\prime}(t)y^{\prime}(t)}{x^{\prime}(t)^3}+\left\lbrace 1 +\left( \frac{y^{\prime}(t)}{x^{\prime}(t)} \right)^2\right\rbrace \cdot\frac{x^{\prime\prime}(t)}{x^{\prime}(t)^2}=0 $$ $$ \frac{x^{\prime}(t)y^{\prime}(t)y^{\prime\prime}(t)-x^{\prime\prime}(t)y^{\prime}(t)^2}{x^{\prime}(t)^4} +\frac{x^{\prime\prime}(t)}{x^{\prime}(t)^2} +\frac{x^{\prime\prime}(t)y^{\prime}(t)^2}{x^{\prime}(t)^4}=0 $$ $$ y^{\prime}(t)y^{\prime\prime}(t)+x^{\prime}(t)x^{\prime\prime}(t)=0 $$

式$(20)$の導出

$$ y^{\prime}(t)y^{\prime\prime}(t)+x^{\prime}(t)x^{\prime\prime}(t)=0 $$ $$ a_y(a_yt+b_y)+a_x(a_xt+b_x)=0 $$ $$ (a_x^2+a_y^2)t+a_xb_x+a_yb_y=0 $$ $$ t=-\frac{a_xb_x+a_yb_y}{a_x^2+a_y^2} $$