通常は一つのレンダーターゲットに対して描画を行います。これに対し、MRT(Multiple Render Target)では複数のレンダーターゲットへ一度に描画することができます。このMRTをRenderFeature内でCommandBufferを使用して実行します。これは、Library¥PackageCache¥com.unity.render-pipelines.universal@7. […]
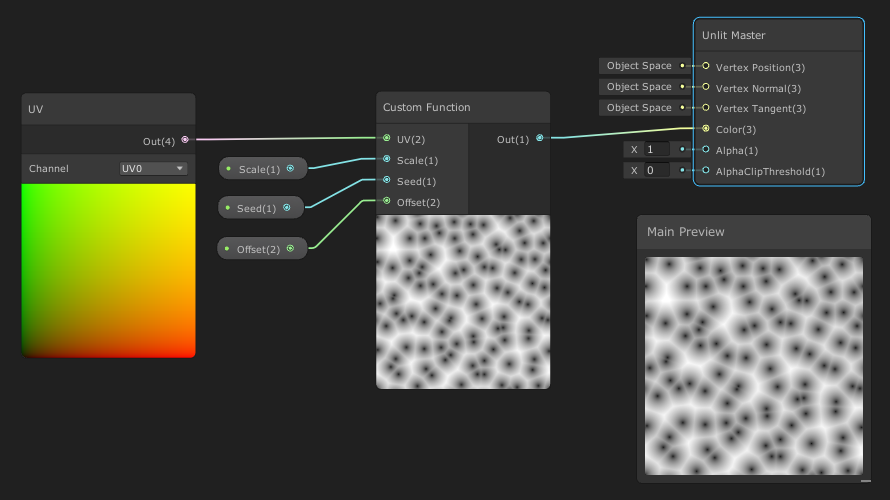
Unityではシェーダを視覚的に作成できる「Shader Graph」が使用できます。このShader Graphでは様々なノードが利用でき、それらを繫げることでシェーダを作成します。このノードの中にCustom Function Nodeがあり、これを利用することでオリジナルのノードを作成することができます。 ノードへ直接記述する方法 Shader Graphを開き、Custom Funct […]
パーリンノイズのタイリング 九個のQuadを並べ、シェーダでノイズ2(パーリンノイズ)で作成したパーリンノイズを生成すると このように、境界ができてしまいます。この原因と解決法を探るため、一次元パーリンノイズを並べたグラフと作成しました。 グラフの中央が境界となっています。パーリンノイズは青色の直線と赤色の直線を補間することにより求めています。このグラフより、青色と赤色の直線は一つの直線となって […]
前回の記事(海洋シェーダ(反射と屈折))では、海面に反射して映るオブジェクトや海中の屈折して見えるオブジェクトを追加しました。今回は、海面に生じる泡の追加を行いました。 波の高さにより泡を生成 波が特定の高さになったときに泡を発生させます。波ごとに高さの判定を行っていますが、その際、波の振幅を計算から除外しています。これにより、振幅が低い波でも泡が発生するように処理をしています。また、泡のテク […]
前回の記事(海洋シェーダ(海の色))では、ノイズで変形させたゲルストナー波によって生成された波に、フレネル反射等を追加することで海を表現しました。この海へ、海面に反射して映るオブジェクトや海中にあるオブジェクトが透過して見える様子を追加しました。 海面の反射 以前作成した平面の鏡面反射を利用して、海面に反射して映る画像を取得します。取得した画像をそのまま表示するのではなく、スクリーン座標を海の […]
前回の記事(海洋シェーダ(波の形))では、ゲルストナー波をノイズで変形させることで 海洋における波の形を作成しました。この波に、フレネル反射等を追加することによって海の色を表現します。 基本の色 海の基本となる色(_SeaBaseColor)にランバート反射で凹凸を付けています。また、波の高さ(wave_height)によって色を変えるために、_SeaShallowColor * wave_h […]
以前、ゲルストナー波(Gerstner Wave)についての記事を掲載しました。このゲルストナー波を用いて海の波をシェーダで作成しました。 ゲルストナー波(8個) shader 単純にゲルストナー波を単純に8個組み合わせるシェーダです。法線は近接する頂点を利用して計算しています。また、ランバート反射によって波の凹凸が分かるように処理をしています。 [crayon-686319ba82b3a65 […]
以前、Textureを合成するShaderであるテクスチャに他のテクスチャを合成する方法を掲載しました。この時は、uv座標を使用していましたが、今回はワールド座標を用いてテクスチャの合成を行います。 shader ここに掲載しているshaderのuv座標をワールド座標(x,z)へ変更したshaderです。このshaderにおいて_PaintPositionのy成分をz座標として使用しています。 […]
太陽光が大気へ突入すると散乱が起こります。この散乱をシェーダーでシミュレーションすることで、空の色を描画することができます。この記事では、GPU Gems 2:Chapter 16. Accurate Atmospheric Scatteringを参考にシェーダーを作成しました。 シェーダーの作成 shader 作成したシェーダーは以下の通りです。GPU Gem2のコードから大きな変更はありま […]
シェーダで頂点を移動すると、元の法線ベクトルは使用できなくなります。そのため、法線ベクトル を再計算する必要があります。法線ベクトルは隣接する頂点もしくはハイトマップから計算することができます。 隣接する頂点を利用する方法 法線ベクトルは、ある点とその近傍の二点の座標を用いることで求めることができます。 ある点 \(P\) における法線ベクトルを求めるには、点 \(P\) から接ベクトル方向へ […]