B-スプライン曲線の導関数

1. 一次導関数
2. t次導関数
3. メモ

一次導関数

n次B-スプライン曲線

n次B-スプライン曲線の式を以下に示します。mはノットベクトルの数です。

$$ \begin{align} \begin{split} &S(u)=\sum_{j=0}^{m-n-2}P_jb_{j,n}(u)\\\\ &b_{j,0}(u):=\begin{cases} 1 \hspace{10pt} if \hspace{10pt} u_j\leq u\lt u_{j+1}\\ 0 \hspace{10pt} otherwise \end{cases} ,\hspace{10pt} j=0,..,m-2\\ &b_{j,k}(u):=\frac{u-u_j}{u_{j+k}-u_j}b_{j,k-1}(u)+\frac{u_{j+k+1}-u}{u_{j+k+1}-u_{j+1}}b_{j+1,k-1}(u), \hspace{10pt} j=0,..,m-k-2 \end{split} \tag{1} \end{align} $$

基底関数$b_{j,n}$の微分

　式$(1)$より、B-スプライン曲線の導関数は基底関数の$b_{j,n}(u)$の導関数$b’_{j,n}(u)$を求めればよいことが分かります。よって、$b_{j,n}(u)$の微分を行います。

$$ \begin{align} b_{j,n}’&=\left[\frac{u-u_j}{u_{j+n}-u_j}b_{j,n-1}(u)\right]’+\left[\frac{u_{j+n+1}-u}{u_{j+n+1}-u_{j+1}}b_{j+1,n-1}(u)\right]’\\\\ &=\frac{1}{u_{j+n}-u_j}b_{j,n-1}(u)+\frac{u-u_j}{u_{j+n}-u_j}b’_{j,n-1}(u)\\\\ &-\frac{1}{u_{j+n+1}-u_{j+1}}b_{j+1,n-1}(u)+\frac{u_{j+n+1}-u}{u_{j+n+1}-u_{j+1}}b’_{j+1,n-1}(u)\\\\ \end{align} $$

これより、$b’_{j,n}(u)$は以下の式となります。

\begin{align} \begin{split} b’_{j,n}(u)&=\frac{1}{u_{j+n}-u_j}\left\{b_{j,n-1}(u)+(u-u_j)b’_{j,n-1}(u)\right\}\\\\ &-\frac{1}{u_{j+n+1}-u_{j+1}}\left\{b_{j+1,n-1}(u)-(u_{j+n+1}-u)b’_{j+1,n-1}(u)\right\} \end{split} \tag{2} \end{align}

$b’_{j,1}(u)$

式$(2)$より、$b’_{j,1}(u)$は以下の式となります。

$$ b’_{j,1}(u)=\frac{1}{u_{j+1}-u_j}b_{j,0}(u)-\frac{1}{u_{j+2}-u_{j+1}}b’_{j+1,0}(u) \tag{3} $$

$b’_{j,2}(u)$

式$(2)$より、$b’_{j,2}(u)$は

$$ \begin{align} b’_{j,2}(u)&=\frac{1}{u_{j+2}-u_j}\left\{b_{j,1}(u)+(u-u_j)b’_{j,1}(u)\right\}\\\\ &-\frac{1}{u_{j+3}-u_{j+1}}\left\{b_{j+1,1}(u)-(u_{j+3}-u)b’_{j+1,1}(u)\right\} \end{align} $$

となります。この式へ式$(3)$を代入すると

$$ \begin{align} b’_{j,2}(u)&=\frac{1}{u_{j+2}-u_j}\left\{b_{j,1}(u)+\frac{u-u_j}{u_{j+1}-u_j}b_{j,0}(u)-\frac{u-u_j}{u_{j+2}-u_{j+1}}b_{j+1,0}(u)\right\}\\\\ &-\frac{1}{u_{j+3}-u_{j+1}}\left\{b_{j+1,1}(u)-\frac{u_{j+3}-u}{u_{j+2}-u_{j+1}}b_{j+1,0}(u)+\frac{u_{j+3}-u}{u_{j+3}-u_{j+2}}b_{j+2.0}(u)\right\} \end{align} $$

よって（詳しくはメモ1）

$$ \begin{align} b’_{j,2}(u)&=\frac{1}{u_{j+2}-u_j}\left\{b_{j,1}(u)+\frac{u-u_j}{u_{j+1}-u_j}b_{j,0}(u)+\frac{u_{u+2}-u}{u_{j+2}-u_{j+1}}b_{j+1,0}(u)\right\}\\\\ &-\frac{1}{u_{j+3}-u_{j+1}}\left\{b_{j+1,1}(u)+\frac{u-u_{j+1}}{u_{j+2}-u_{j+1}}b_{j+1,0}(u)+\frac{u_{j+3}-u}{u_{j+3}-u_{j+2}}b_{j+2.0}(u)\right\} \end{align} $$

式$(1)$より、$b_{j,1}(u)$及び$b_{j+1,1}(u)$は

$$ \begin{align} &b_{j,1}(u)=\frac{u-u_j}{u_{j+1}-u_j}b_{j,0}(u)+\frac{u_{j+2}-u}{u_{j+2}-u_{j+1}}b_{j+1,0}(u)\\\\ &b_{j+1,1}(u)=\frac{u-u_{j+1}}{u_{j+2}-u_{j+1}}b_{j+1,0}(u)+\frac{u_{j+3}-u}{u_{j+3}-u_{j+2}}b_{j+2,0}(u) \end{align} $$

なので、$b’_{j,2}(u)$は以下の式となります。

$$ b’_{j,2}(u)=\frac{2}{u_{j+2}-u_j}b_{j,1}(u)-\frac{2}{u_{j+3}-u_{j+1}}b_{j+1,1}(u) \tag{4} $$

$b’_{j,3}(u)$

式$(2)$より、$b’_{j,3}(u)$は

$$ \begin{align} b’_{j,3}(u)&=\frac{1}{u_{j+3}-u_j}\left\{b_{j,2}(u)+(u-u_j)b’_{j,2}(u)\right\}\\\\ &-\frac{1}{u_{j+4}-u_{j+1}}\left\{b_{j+1,2}(u)+(u_{j+4}-u)b’_{j+1,2}(u)\right\} \end{align} $$

となります。この式へ式(4)を代入すると

$$ \begin{align} b’_{j,3}(u)&=\frac{1}{u_{j+3}-u_j}\left\{b_{j,2}(u)+\frac{2(u-u_j)}{u_{j+2}-u_j}b_{j,1}(u)-\frac{2(u-u_j)}{u_{j+3}-u_{j+1}}b_{j+1,1}(u)\right\}\\\\ &-\frac{1}{u_{j+4}-u_{j+1}}\left\{b_{j+1,2}(u)-\frac{2(u_{j+4}-u)}{u_{j+3}-u_{j+1}}b_{j+1,1}(u)+\frac{2(u_{j+4}-u)}{u_{j+4}-u_{j+2}}b_{j+2,1}(u)\right\}\\\\ \end{align} $$

よって（詳しくはメモ2）

$$ \begin{align} b’_{j,3}(u)&=\frac{1}{u_{j+3}-u_j}\left\{b_{j,2}(u)+\frac{2(u-u_j)}{u_{j+2}-u_j}b_{j,1}(u)+\frac{2(u_{j+3}-u)}{u_{j+3}-u_{j+1}}b_{j+1,1}(u)\right\}\\\\ &-\frac{1}{u_{j+4}-u_{j+1}}\left\{b_{j+1,2}(u)+\frac{2(u-u_{j+1})}{u_{j+3}-u_{j+1}}b_{j+1,1}(u)+\frac{2(u_{j+4}-u)}{u_{j+4}-u_{j+2}}b_{j+2,1}(u)\right\} \end{align} $$

式$(1)$より、$b_{j,2}(u)$及び$b_{j+2,2}(u)$は

$$ \begin{align} &b_{j,2}(u)=\frac{u-u_j}{u_{j+2}-u_j}b_{j,1}(u)+\frac{u_{j+3}-u}{u_{j+3}-u_{j+1}}b_{j+1,1}(u)\\\\ &b_{j+2,2}(u)=\frac{u-u_{j+1}}{u_{j+3}-u_{j+1}}b_{j+1,1}(u)+\frac{u_{j+4}-u}{u_{j+4}-u_{j+2}}b_{j+2,1}(u) \end{align} $$

なので、$b’_{j,3}(u)$は以下の式となります。

$$ b’_{j,3}(u)=\frac{3}{u_{j+3}-u_j}b_{j,2}(u)-\frac{3}{u_{j+4}-u_{j+1}}{b_{j+1,2}(u)} $$

$b’_{j,n}(u)$

$b’_{j,1}(u)$、$b’_{j,2}(u)$及び$b’_{j,3}(u)$より$b’_{j,n}(u)$は以下の式となります。

$$ b’_{j,n}(u)=\frac{n}{u_{j+n}-u_j}b_{j,n-1}-\frac{n}{u_{j+n+1}-u_{j+1}}{b_{j+1,n-1}} \tag{5} $$

確認

　式$(5)$が正しいか確認します。式$(1)$より$b’_{j,n+1}(u)$は

$$ \begin{align} b’_{j,n+1}(u)&=\frac{1}{u_{j+n+1}-u_j}\left\{b_{j,n}(u)+(u-u_j)b’_{j,n}(u)\right\}\\\\ &-\frac{1}{u_{j+n+2}-u_{j+1}}\left\{b_{j+1,n}(u)+(u_{j+n+2}-u)b’_{j+1,n}(u)\right\} \end{align} $$

式$(5)$より、上式へ以下の$b’_{j,n}(u)$及び$b’_{j,n+1}(u)$を代入すると

$$ \begin{align} &b’_{j,n}(u)=\frac{n}{u_{j+n}-u_j}b_{j,n-1}(u)-\frac{n}{u_{j+n+1}-u_{j+1}}b_{j+1,n-1}(u)\\\\ &b’_{j+1,n}(u)=\frac{n}{u_{j+n+1}-u_{j+1}}b_{j+1,n-1}(u)-\frac{n}{u_{j+n+2}-u_{j+2}}b_{j+2,n-1}(u) \end{align} $$

以下の式となります。

$$ \begin{align} b’_{j,n+1}(u)&=\frac{1}{u_{j+n+1}-u_j}\left\{b_{j,n}(u)+\frac{n(u-u_j)}{u_{j+n}-u_j}b_{j,n-1}(u)-\frac{n(u-u_j)}{u_{j+n+1}-u_{j+1}}b_{j+1,n-1}(u)\right\}\\\\ &-\frac{1}{u_{j+n+2}-u_{j+1}}\left\{b_{j+1,n}(u)+\frac{n(u_{j+n+2}-u)}{u_{j+n+1}-u_{j+1}}b_{j+1,n-1}(u)+\frac{n(u_{j+n+2}-u)}{u_{j+n+2}-u_{j+2}}b_{j+2,n-1}(u)\right\}\\\\ \end{align} $$

この式を整理すると（詳しくはメモ3）

$$ \begin{align} b’_{j,n+1}&=\frac{1}{u_{j+n+1}-u_j}\left\{b_{j,n}(u)+\frac{n(u-u_j)}{u_{j+n}-u_j}b_{j,n-1}(u)+\frac{n(u_{j+n+1}-u)}{u_{j+n+1}-u_{j+1}}b_{j+1,n-1}(u)\right\}\\\\ &-\frac{1}{u_{j+n+2}-u_{j+1}}\left\{b_{j+1,n}(u)+\frac{n(u-u_{j+1})}{u_{j+n+1}-u_{j+1}}b_{j+1,n-1}(u)+\frac{n(u_{j+n+2}-u)}{u_{j+n+2}-u_{j+2}}b_{j+2,n-1}(u)\right\}\\\\ \end{align} $$

となります。式$(1)$より、$b_{j,n}(u)$及び$b_{j,n+1}(u)$は

$$ \begin{align} &b_{j,n}(u)=\frac{u-u_j}{u_{j+n}-u_j}b_{j,n-1}(u)+\frac{u_{j+n+1}-u}{u_{j+n+1}-u_{j+1}}b_{j+1,n-1}(u)\\\\ &b_{j+1,n}(u)=\frac{u-u_{j+1}}{u_{j+n+1}-u_{j+1}}b_{j+1,n-1}(u)+\frac{u_{j+n+2}-u}{u_{j+n+2}-u_{j+2}}b_{j+2,n-1}(u) \end{align} $$

なので、$b’_{j,n+1}(u)$は以下の式となります。

$$ \begin{align} b’_{j,n+1}(u)&=\frac{n+1}{u_{j+n+1}-u_j}b_{j,n}(u)-\frac{n+1}{u_{j+n+2}-u_{j+1}}b_{j+1,n}(u)\\\\ \end{align} $$

この式は、式$(5)$に一致しており式$(5)$が正しいことが確認できました。

B-スプライン曲線の一次導関数

以上より、スプライン曲線の導関数は以下の式となります。

$$ \begin{align} \begin{split} &S'(u)=\sum_{j=0}^{m-n-2}P_jb’_{j,n}(u)\\\\ &b’_{j,n}(u)=\frac{n}{u_{j+n}-u_j}b_{j,n-1}-\frac{n}{u_{j+n+1}-u_{j+1}}{b_{j+1,n-1}}\\\\ &b_{j,0}(u):=\begin{cases} 1 \hspace{10pt} if \hspace{10pt} u_j\leq u\lt u_{j+1}\\ 0 \hspace{10pt} otherwise \end{cases} ,\hspace{10pt} j=0,..,m-2\\ &b_{j,k}(u):=\frac{u-u_j}{u_{j+k}-u_j}b_{j,k-1}(u)+\frac{u_{j+k+1}-u}{u_{j+k+1}-u_{j+1}}b_{j+1,k-1}(u), \hspace{10pt} j=0,..,m-k-2 \end{split} \tag{6} \end{align} $$

グラフ

　求めた一次導関数により、B-スプライン曲線の接線を描画したグラフです。

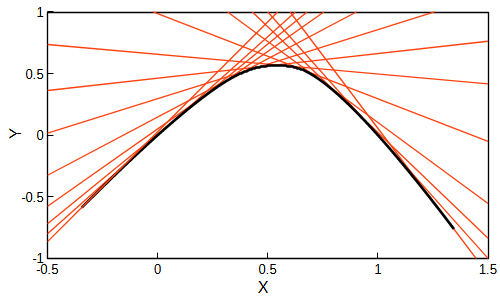
t次導関数

　式$(6)$よりt次導関数は

$$ \begin{align} \begin{split} &S^{(t)}(u)=\sum_{j=0}^{m-n-2}P_jb^{(t)}_{j,n}(u)\\\\ &b^{(t)}_{j,n}(u)=\frac{n}{u_{j+n}-u_j}b^{(t-1)}_{j,n-1}-\frac{n}{u_{j+n+1}-u_{j+1}}{b^{(t-1)}_{j+1,n-1}}\\\\ &b_{j,0}(u):=\begin{cases} 1 \hspace{10pt} if \hspace{10pt} u_j\leq u\lt u_{j+1}\\ 0 \hspace{10pt} otherwise \end{cases} ,\hspace{10pt} j=0,..,m-2\\ &b_{j,k}(u):=\frac{u-u_j}{u_{j+k}-u_j}b_{j,k-1}(u)+\frac{u_{j+k+1}-u}{u_{j+k+1}-u_{j+1}}b_{j+1,k-1}(u), \hspace{10pt} j=0,..,m-k-2 \end{split} \tag{7} \end{align} $$

メモ

1

$$ \begin{align} &\frac{u_j-u}{(u_{j+2}-u_j)(u_{j+2}-u_{j+1})}b_{j+1,0}(u)+\frac{u_{j+3}-u}{(u_{j+3}-u_{j+1})(u_{j+2}-u_{j+1})}b_{j+1,0}(u)\\\\ &=\frac{(u_j-u)(u_{j+3}-u_{j+1})+(u_{j+3}-u)(u_{j+2}-u_j)}{(u_{j+2}-u_j)(u_{j+3}-u_{j+1})(u_{j+2}-u_{j+1})}b_{j+1,0}(u)\\\\ &=\frac{-u(u_{j+3}-u_{j+1})+u_{j+2}u_{j+3}-u(u_{j+2}-u_j)-u_ju_{j+1}}{(u_{j+2}-u_j)(u_{j+3}-u_{j+1})(u_{j+2}-u_{j+1})}b_{j+1,0}(u)\\\\ &=\frac{-u(u_{j+3}-u_{j+1})+u_{j+2}u_{j+3}-u_{j+1}u_{j+2}}{(u_{j+2}-u_j)(u_{j+3}-u_{j+1})(u_{j+2}-u_{j+1})}b_{j+1,0}(u)\\\\ &+\frac{-u(u_{j+2}-u_j)-u_ju_{j+1}+u_{j+1}u_{j+2}}{(u_{j+2}-u_j)(u_{j+3}-u_{j+1})(u_{j+2}-u_{j+1})}b_{j+1,0}(u)\\\\ &=\frac{(u_{j+2}-u)(u_{j+3}-u_{j+1})}{(u_{j+2}-u_j)(u_{j+3}-u_{j+1})(u_{j+2}-u_{j+1})}b_{j+1,0}(u)\\\\ &-\frac{(u-u_{j+1})(u_{j+2}-u_j)}{(u_{j+2}-u_j)(u_{j+3}-u_{j+1})(u_{j+2}-u_{j+1})}b_{j+1,0}(u)\\\\ &=\frac{u_{j+2}-u}{(u_{j+2}-u_j)(u_{j+2}-u_{j+1})}b_{j+1,0}(u)-\frac{u_{j+k+1}-u}{(u_{j+3}-u_{j+1})(u_{j+2}-u_{j+1})}b_{j+1,0}(u) \end{align} $$

2

$$ \begin{align} &\frac{u_j-u}{(u_{j+3}-u_j)(u_{j+3}-u_{j+1})}b_{j+1,1}(u)+\frac{u_{j+4}-u}{(u_{j+4}-u_{j+1})(u_{j+3}-u_{j+1})}b_{j+1,1}(u)\\\\ &=\frac{(u_j-u)(u_{j+4}-u_{j+1})+(u_{j+4}-u)(u_{j+3}-u_j)}{(u_{j+3}-u_j)(u_{j+3}-u_{j+1})(u_{j+4}-u_{j+1})}b_{j+1,1}(u)\\\\ &=\frac{-u(u_{j+4}-u_{j+1})+u_{j+3}u_{j+4}-u(u_{j+3}-u_{j+1})-u_ju_{j+1}}{(u_{j+3}-u_j)(u_{j+3}-u_{j+1})(u_{j+4}-u_{j+1})}b_{j+1,1}(u)\\\\ &=\frac{-u(u_{j+4}-u_{j+1})+u_{j+3}u_{j+4}-u_{j+1}u_{j+3}}{(u_{j+3}-u_j)(u_{j+3}-u_{j+1})(u_{j+4}-u_{j+1})}b_{j+1,1}(u)\\\\ &+\frac{-u(u_{j+3}-u_{j+1})-u_ju_{j+1}+u_{j+1}u_{j+3}}{(u_{j+3}-u_j)(u_{j+3}-u_{j+1})(u_{j+4}-u_{j+1})}b_{j+1,1}(u)\\\\ &=\frac{(u_{j+3}-u)(u_{j+4}-u_{j+1})}{(u_{j+3}-u_j)(u_{j+3}-u_{j+1})(u_{j+4}-u_{j+1})}b_{j+1,1}(u)\\\\ &+\frac{(u_{j+1}-u)(u_{j+3}-u_{j+1})}{(u_{j+3}-u_j)(u_{j+3}-u_{j+1})(u_{j+4}-u_{j+1})}b_{j+1,1}(u)\\\\ &=\frac{u_{j+3}-u}{(u_{j+3}-u_j)(u_{j+3}-u_{j+1})}b_{j+1,1}(u)+\frac{u_{j+1}-u}{(u_{j+3}-u_j)(u_{j+4}-u_{j+1})}b_{j+1,1}(u)\\\\ \end{align} $$

3

$$ \begin{align} &\frac{u_j-u}{(u_{j+n+1}-u_j)(u_{j+n+1}-u_{j+1})}b_{j+1,n-1}(u)+\frac{u_{j+n+2}-u}{(u_{j+n+2}-u_{j+1})(u_{j+n+1}-u_{j+1})}b_{j+1,n-1}(u)\\\\ &=\frac{(u_j-u)(u_{j+n+2}-u_{j+1})+(u_{j+n+2}-u)(u_{j+n+1}-u_j)}{(u_{j+n+1}-u_j)(u_{j+n+1}-u_{j+1})(u_{j+n+2}-u_{j+1})}b_{j+1,n-1}(u)\\\\ &=\frac{-u(u_{j+n+2}-u_{j+1})+u_{j+n+1}u_{j+n+2}-u(u_{j+n+1}-u_j)-u_ju_{j+1}}{(u_{j+n+1}-u_j)(u_{j+n+1}-u_{j+1})(u_{j+n+2}-u_{j+1})}b_{j+1,n-1}(u)\\\\ &=\frac{-u(u_{j+n+2}-u_{j+1})+u_{j+n+1}u_{j+n+2}-u_{j+1}u_{j+n+1}}{(u_{j+n+1}-u_j)(u_{j+n+1}-u_{j+1})(u_{j+n+2}-u_{j+1})}b_{j+1,n-1}(u)\\\\ &+\frac{-u(u_{j+n+1}-u_j)-u_ju_{j+1}+u_{j+1}u_{j+n+1}}{(u_{j+n+1}-u_j)(u_{j+n+1}-u_{j+1})(u_{j+n+2}-u_{j+1})}b_{j+1,n-1}(u)\\\\ &=\frac{(u_{j+n+1}-u)(u_{j+n+2}-u_{j+1})}{(u_{j+n+1}-u_j)(u_{j+n+1}-u_{j+1})(u_{j+n+2}-u_{j+1})}b_{j+1,n-1}(u)\\\\ &+\frac{(u_{j+1}-u)(u_{j+n+1}-u_j)}{(u_{j+n+1}-u_j)(u_{j+n+1}-u_{j+1})(u_{j+n+2}-u_{j+1})}b_{j+1,n-1}(u)\\\\ &=\frac{u_{j+n+1}-u}{(u_{j+n+1}-u_j)(u_{j+n+1}-u_{j+1})}b_{j+1,n-1}(u)+\frac{u_{j+1}-u}{(u_{j+n+1}-u_{j+1})(u_{j+n+2}-u_{j+1})}b_{j+1,n-1}(u) \end{align} $$