二次スB-プライン曲線の最接近点(展開した式を利用)

前回求めた式を利用して制御点が5点の場合における二次B-スプライン曲線の最接近点を求めます。
式の導出
前回求めた二次B-スプライン曲線の式は
$$ \begin{align} S&(u)=au^2+bu+c \tag{1}\\\\ a&=9b_{2,0}P_0+(9b_{1,0}-\frac{27}{2}b_{2,0}+\frac{9}{2}b_{3,0})P_1\\\\ &+(\frac{9}{2}b_{2,0}-9b_{3,0}+\frac{9}{2}b_{4,0})P_2+(\frac{9}{2}b_{3,0}-\frac{27}{2}b_{4,0})P_3+9P_4b_{4,0}\\\\ b&=-6P_0b_{2,0}+(6b_{2,0}-6b_{3,0})P_1+(9b_{3,0}-9b_{4,0})P_2\\\\ &+(-3b_{3,0}+21b_{4,0})P_3-12P_4b_{4,0}\\\\ c&=P_0b_{2,0}+2P_1b_{3,0}+(-\frac{3}{2}b_{3,0}+\frac{9}{2}b_{4,0})P_2\\\\ &+(\frac{1}{2}b_{3,0}-\frac{15}{2}b_{4,0})P_3+4P_4b_{4,0} \end{align} $$です。点\((x_0,y_0)\)と二次B-スプライン曲線の距離は
$$ D=(x_0-S_x(u))^2+(y_0-S_y(u))^2 \tag{2} $$であるので、式\((2)\)へ式\((1)\)代入し、整理すると
$$ D=du^4+eu^3+fu^2+gu+h \tag{3} $$となります。ただし
$$ \begin{align} &d=a_x^2+a_y^2,\ e=2(a_xb_x+a_yb_y)\\\\ &f=2a_xc_x+b_x^2-2a_xx_0+2a_yc_y+b_y^2-2a_yy_0\\\\ &g=2b_xc_x-2b_xx_0+2b_yc_y-2b_yy_0\\\\ &h=(c_x-x_0)^2+(c_y-y_0)^2 \end{align} $$です。式\((3)\)の極値を求めることで最接近点を求めます。よって、以下の式の解をニュートン法により求めることで最接近点を見つけます。
$$ D’=4du^3+3eu^2+2fu+gu=0 \tag{4} $$ニュートン法
ニュートン法は以下の式で繰り返し\(x_{n+1}\)を求めることで解へ収束します。
$$ x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)} \tag{5} $$\(D’\)は三次方程式なので解が最大3個の実数解が存在します。ニュートン法によって他の解を求めるには、上記の方程式によって得られた解\(α_1\)を用いて、\(f_1(x)\)を作成します。この式を用いることで他の解を求めることができます。
$$ \begin{align} &f_1(x)=\frac{f(x)}{x-α_1} \\\\ &x_{n+1}=x_n-\frac{f_1(x_n)}{f_1′(x_n)} \tag{6} \end{align} $$さらに、上記の方程式によって解\(α_2\)が求まった場合、残りの解は以下の式によって求めることができます。
$$ \begin{align} &f_2(x)=\frac{f(x)}{(x-α_1)(x-α_2)} \\\\ &x_{n+1}=x_n-\frac{f_2(x_n)}{f_2′(x_n)} \tag{7} \end{align} $$これらの式より三個の解を求めることができます。よって式\((4)\)の一つ目の解は式\((5)\)より
$$ u_{n+1}=u_n-\frac{D’}{D^{\prime\prime}}=u_n-\frac{4du_n^3+3eu_n^2+2fu_n+gu_n}{12du_n^2+6eu_n+2f} \tag{8} $$によって求めることができます。次の解を求めるには式\((6)\)より
$$ u_{n+1}=u_n-\frac{D_1′}{D_1^{\prime\prime}} \tag{9} $$ $$ \begin{align} &D’_1=\frac{4du_n^3+3eu_n^2+2fu_n+g}{u_n-α_1} \tag{10}\\\\ &D^{\prime\prime}_1=\frac{8du_n^3+(3e-12α_1d)u_n^2-6α_1eu_n-2α_1f-g}{(u_n-α_1)^2} \tag{11} \end{align} $$式\((7)\)より最後の解は以下の式によって求まります。
$$ u_{n+1}=u_n-\frac{D_2′}{D_2^{\prime\prime}} \tag{12} $$ $$ \begin{align} &D’_2=\frac{4du^3+6eu^2+2fu+g}{(u-α_1)(u-α_2)} \tag{13}\\\\ &D^{\prime\prime}_2=\frac{4du^4-8tdu^3+(12nd-2f-3te)u^2+(6ne-2g)u+2nf+tg}{(u-α_1)^2(u-α_2)^2} \tag{14}\\\\ &t=α_1+α_2,\ n=α_1α_2 \end{align} $$問題点
ノットベクトル\(u_j\)と基底関数\(b_{j,0}\)より\(u \lt 0\)と\(1 \leq u\)において、二次B-スプライン曲線は常に0となることが分かります。
$$ u_j=\{0,0,0,\frac{1}{3},\frac{2}{3},1,1,1\} $$ $$ b_{j,0}(u):=\begin{cases} 1 \hspace{10pt} if \hspace{10pt} u_j\leq u\lt u_{j+1}\\ 0 \hspace{10pt} otherwise \end{cases} $$ニュートン法を利用する場合、計算過程で\(u \lt 0\)と\(1 \leq u\)となる可能性があります。よって、この条件のままではニュートン法によって解が求められない場合が出てきます。そこで、以下のように\(b_{j,0}(u)\)の条件を変更しました。
$$ \begin{align} &b_{2,0}(u):=\begin{cases} 1 \hspace{10pt} if \hspace{10pt} u\lt u_3\\ 0 \hspace{10pt} otherwise \end{cases}\\ &b_{4,0}(u):=\begin{cases} 1 \hspace{10pt} if \hspace{10pt} u_4\leq u\\ 0 \hspace{10pt} otherwise \end{cases}\\ \end{align} $$この基底関数を用いて、以下の制御点によってグラフを作成しました。
$$ \begin{align} &P_0=(0,0),\ P_1=(0.25,0.4), \ P_2=(0.5,0.6)\\ &P_3=(0.75,0.5), \ P_4=(1.0,0) \end{align} $$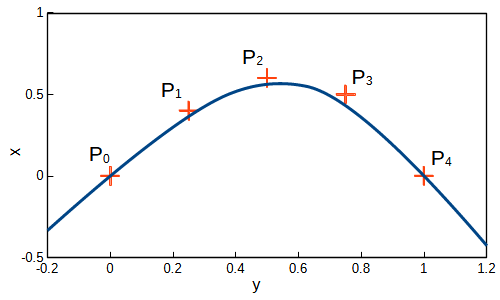
\(u \lt 0\)と\(1 \leq u\)の範囲も二次B-スプライン曲線を求めることができています。
最接近点
最接近点を探す初期位置をQ\((0.8,\ 0)\)とします。式\((10)\)より、\(D’\)を求めると以下のようになります。
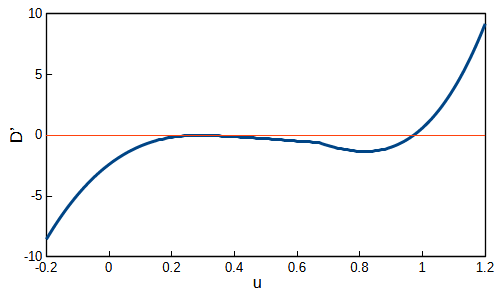
\(D’=0\)である赤い線と重なっている部分があります。この部分を拡大すると
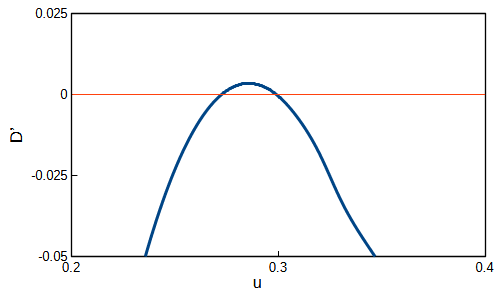
となります。これより、\(D’=0\)となる解は3個存在することが確認できました。\(D^{\prime\prime}\)が正しく求まっているか確認するためにグラフを作成しました。
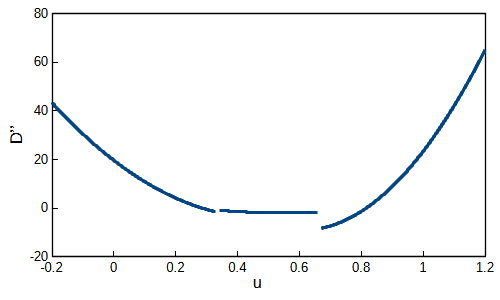
急に値が変化している箇所がありますが、その部分が区間のの境目となっています。式\((8)\)によって解を求めたところ\(α_1=0.2724835\)となりました。次に式\((9)\)によって次の解を求めます。\(D_1’\)をグラフにすると
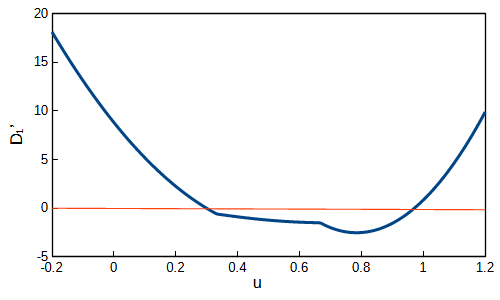
となります。グラフから\(D_1’=0\)となる解は2個存在することが確認できます。これより、\(D_1’=0\)は二次方程式になっていることが分かります。また、\(D_1^{\prime\prime}\)のグラフは以下のようになります。
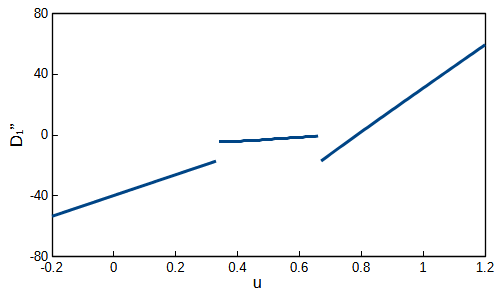
直線で構成されており\(D_1^{\prime\prime}\)が問題なく求まっていることが確認できました。式\((9)\)によって解を求めた結果\(α_2=0.9715583\)となりました。最後に式\((12)\)によって3個目の解を求めます。\(D_2’\)をグラフにすると
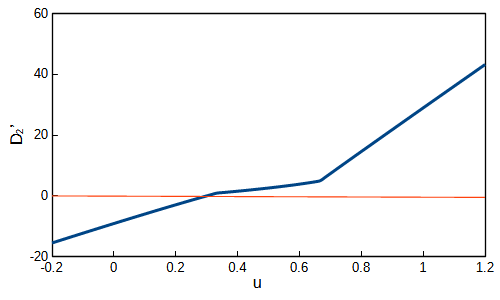
となります。直線となっており解が一つであることが確認できます。また、\(D_2^{\prime\prime}\)をグラフは以下のようになります。
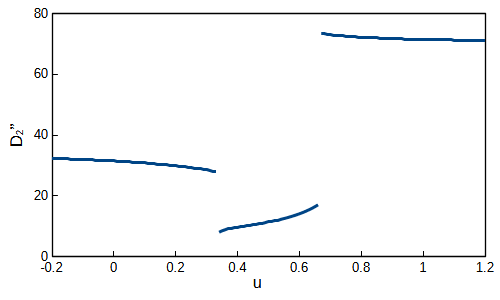
式\((12)\)によって求めた解は\(α_3=0.2991613\)となりました。これらの解によって座標値を求めグラフへ描画すると
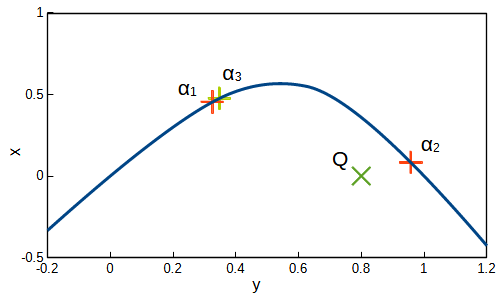
となり、\(α_2=0.9715583\)が求める解であることがわかりました。これより、最接近点は\((0.9582475,0.0820489)\)と求まりました。
-
前の記事
二次B-スプライン曲線の最接近点(式の展開) 2023.05.13
-
次の記事
B-スプライン曲線の導関数 2023.05.20




コメントを書く