二次B-スプライン曲線の最接近点(式の展開)

式の展開
制御点が5点の二次B-スプライン曲線の式は
$$ S(u)=\sum_{j=0}^{4}P_jb_{j,2}(u) \tag{1} $$ $$ \begin{align} &b_{j,0}(u):=\begin{cases} 1 \hspace{10pt} if \hspace{10pt} u_j\leq u\lt u_{j+1}\\ 0 \hspace{10pt} otherwise \end{cases} ,\hspace{10pt} j=0,..,6\\ &b_{j,k}(u):=\frac{u-u_j}{u_{j+k}-u_j}b_{j,k-1}(u)+\frac{u_{j+k+1}-u}{u_{j+k+1}-u_{j+1}}b_{j+1,k-1}(u), \hspace{10pt} j=0,..,6-k \end{align} $$です。これより、基底関数\(b_{j,2}\)は以下となります。
$$ \begin{align} b_{j,2}&=\frac{(u-u_j)^2}{(u_{j+2}-u_j)(u_{j+1}-u_j)}b_{j,0}(u)\\\\ &-\frac{(u-u_{j})(u-u_{j+2})}{(u_{j+2}-u_{j})(u_{j+2}-u_{j+1})}b_{j+1,0}(u)\\\\ &-\frac{(u-u_{j+1})(u-u_{j+3})}{(u_{j+3}-u_{j+1})(u_{j+2}-u_{j+1})}b_{j+1,0}(u)\\\\ &+\frac{(u-u_{j+3})^2}{(u_{j+3}-u_{j+1})(u_{j+3}-u_{j+2})}b_{j+2,0}(u) \tag{2}\\\\ \end{align} $$よって基底関数\(b_{0,2}\)~\(b_{4,2}\)は
$$ \begin{align} b_{0,2}&=\frac{(u-u_0)^2}{(u_2-u_0)(u_1-u_0)}b_{0,0}(u)-\frac{(u-u_0)(u-u_2)}{(u_2-u_0)(u_2-u_1)}b_{1,0}(u)\\\\ &-\frac{(u-u_1)(u-u_3)}{(u_3-u_1)(u_2-u_1)}b_{1,0}(u)+\frac{(u-u_3)^2}{(u_3-u_1)(u_3-u_2)}b_{2,0}(u)\\\\ \end{align} $$ $$ \begin{align} b_{1,2}&=\frac{(u-u_1)^2}{(u_3-u_1)(u_2-u_1)}b_{1,0}(u)-\frac{(u-u_1)(u-u_3)}{(u_3-u_1)(u_3-u_2)}b_{2,0}(u)\\\\ &-\frac{(u-u_2)(u-u_4)}{(u_4-u_2)(u_3-u_2)}b_{2,0}(u)+\frac{(u-u_4)^2}{(u_4-u_2)(u_4-u_3)}b_{3,0}(u)\\\\ \end{align} $$ $$ \begin{align} b_{2,2}&=\frac{(u-u_2)^2}{(u_4-u_2)(u_3-u_2)}b_{2,0}(u)-\frac{(u-u_2)(u-u_4)}{(u_4-u_2)(u_4-u_3)}b_{3,0}(u)\\\\ &-\frac{(u-u_3)(u-u_5)}{(u_5-u_3)(u_4-u_3)}b_{3,0}(u)+\frac{(u-u_5)^2}{(u_5-u_3)(u_5-u_4)}b_{4,0}(u)\\\\ \end{align} $$ $$ \begin{align} b_{3,2}&=\frac{(u-u_3)^2}{(u_5-u_3)(u_4-u_3)}b_{3,0}(u)-\frac{(u-u_3)(u-u_5)}{(u_5-u_3)(u_5-u_4)}b_{4,0}(u)\\\\ &-\frac{(u-u_4)(u-u_6)}{(u_6-u_4)(u_5-u_4)}b_{4,0}(u)+\frac{(u-u_6)^2}{(u_6-u_4)(u_6-u_5)}b_{5,0}(u)\\\\ \end{align} $$ $$ \begin{align} b_{4,2}&=\frac{(u-u_4)^2}{(u_6-u_4)(u_5-u_4)}b_{4,0}(u)-\frac{(u-u_4)(u-u_6)}{(u_6-u_4)(u_6-u_5)}b_{5,0}(u)\\\\ &-\frac{(u-u_5)(u-u_7)}{(u_7-u_5)(u_6-u_5)}b_{5,0}(u)+\frac{(u-u_7)^2}{(u_7-u_5)(u_7-u_6)}b_{6,0}(u)\\\\ \end{align} $$となります。制御点が5点の場合、二次B-スプライン曲線の開一様ノットベクトルは以下のようになります。
$$ u_j=\{0,0,0,\frac{1}{3},\frac{2}{3},1,1,1\} $$\(u_j\)をそれぞれの基底関数に代入し整理すると
$$ \begin{align} &b_{0,2}=(9u^2-6u+1)b_{2,0}\\ &b_{1,2}=(9b_{1,0}-\frac{27}{2}b_{2,0}+\frac{9}{2}b_{3,0})u^2+(6b_{2,0}-6b_{3,0})u+2b_{3,0}\\ &b_{2,2}=(\frac{9}{2}b_{2,0}-9b_{3,0}+\frac{9}{2}b_{4,0})u^2+(9b_{3,0}-9b_{4,0})u-\frac{3}{2}b_{3,0}+\frac{9}{2}b_{4,0}\\ &b_{3,2}=(\frac{9}{2}b_{3,0}-\frac{27}{2}b_{4,0})u^2+(-3b_{3,0}+21b_{4,0})u+\frac{1}{2}b_{3,0}-\frac{15}{2}b_{4,0}\\ &b_{4,2}=(9u^2-12u+4)b_{4,0} \end{align} $$となります。求めた基底関数を式\((1)\)へ代入すると以下の式となります。
$$ S(u)=au^2+bu+c \tag{3} $$ただし、
$$ \begin{align} a&=9b_{2,0}P_0+(9b_{1,0}-\frac{27}{2}b_{2,0}+\frac{9}{2}b_{3,0})P_1\\\\ &+(\frac{9}{2}b_{2,0}-9b_{3,0}+\frac{9}{2}b_{4,0})P_2+(\frac{9}{2}b_{3,0}-\frac{27}{2}b_{4,0})P_3+9P_4b_{4,0}\\\\ b&=-6P_0b_{2,0}+(6b_{2,0}-6b_{3,0})P_1+(9b_{3,0}-9b_{4,0})P_2\\\\ &+(-3b_{3,0}+21b_{4,0})P_3-12P_4b_{4,0}\\\\ c&=P_0b_{2,0}+2P_1b_{3,0}+(-\frac{3}{2}b_{3,0}+\frac{9}{2}b_{4,0})P_2+(\frac{1}{2}b_{3,0}-\frac{15}{2}b_{4,0})P_3+4P_4b_{4,0} \end{align} $$です。
グラフ
以下の制御点を用いてグラフを作成しました。
$$ \begin{align} &p_0=(0,0),\ p_1=(0.25,0.4), \ p_2=(0.5,0.6)\\ &p_3=(0.75,0.5), \ p_4=(1.0,0) \end{align} $$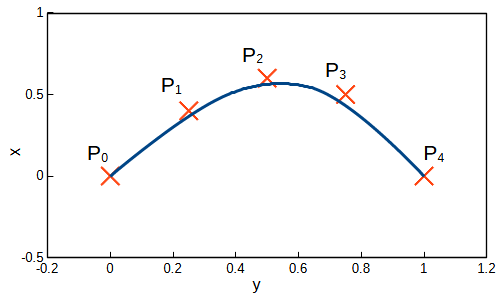
式\((3)\)によって二次B-スプライン曲線が求められることが確認できました。
-
前の記事
ベジェ曲線の最接近点 2023.05.03
-
次の記事
二次スB-プライン曲線の最接近点(展開した式を利用) 2023.05.14




コメントを書く