平面の鏡面反射(Cubemap)

2019.10.14
Unity
script

　以前にReflectionProbeやReflectionMatrixを用いた鏡面反射について記事を掲載しました（平面の鏡面反射）。その際はRenderTextureを用いていましたが、その代わりにCubemapが得られないかとScriptを変更したところ問題が発生しました。CubemapはCamera.RenderToCubemapにより得られますが、これを実行すると、変更したworldToCameraMatrixが元に戻ってしまい反射画像が得られませんでした。そこで、ReflectionMatrixによってworldToCameraMatrixを変更するのではなく、鏡面位置におけるカメラの座標と回転を求め、鏡面反射用のCubemapが得られないか試してみました。

1. 鏡面反射用カメラの座標と回転
2. RenderTextureに変更
- 2.1. Script
- 2.2. 実行結果

鏡面反射用カメラの座標と回転

鏡面位置の座標

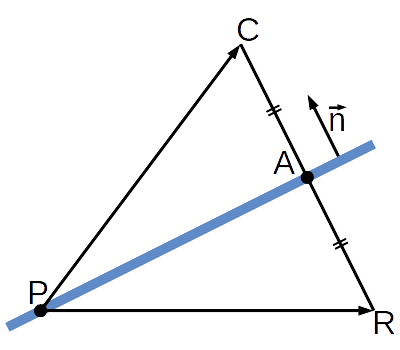
　座標$P$を中心とする平面の法線ベクトル$\vec{n}$及びメインカメラの座標$C$より、点$C$から平面へ垂直に下した線と平面の交点$A$が求まります。そして、ベクトル $\vec{CA}$を求め、交点$A$を$\vec{CA}$で移動するとカメラの鏡面位置$R$が求まります。

図1. 鏡面におけるカメラ座標Cと鏡面位置Rの関係

鏡面位置の座標Rは以下の式より求めることができます。

$$ R=A+A-C=2A-C　\tag{1} $$

まず、交点$A$を求めます。点$C$を通り、$\vec{n}$に平行な直線はベクトル方程式より

$$ \begin{align} \left\{ \begin{array}{l} x&=c_{x}+n_{x}t\\ y&=c_{y}+n_{y}t\\ z&=c_{z}+n_{z}t \end{array} \right.　\tag{2} \end{align} $$

となります。また、平面の方程式は

$$ \begin{align} n_{x}x+n_{y}y+n_{z}z+d=0\\ d=-n_{x}p_{x}-n_{y}p_{y}-n_{z}p_{z} \end{align} \tag{3} $$

です。式$(2)$を式$(3)$へ代入すると

$$ t=-\frac{n_{x}c_{x}+n_{y}c_{y}+n_{z}c_{z}+d}{n_{x}n_{x}+n_{y}n_{y}+n_{z}n_{z}} \tag{4} $$

と求まります。この式を内積を用いて表すと

$$ t=-\frac{\vec{n}\cdot \vec{c}-\vec{n}\cdot \vec{p}}{\vec{n}\cdot \vec{n}} \tag{5} $$

となります。ここで、$\vec{n}$を単位ベクトルとすると

$$ t=\vec{n}\cdot \vec{p}-\vec{n}\cdot \vec{c} \tag{6} $$

となります。この$t$を式$(1)$に代入することで、交点$A$が求まります。求められた点$A$を式$(1)$へ代入するとことで、鏡面反転したカメラの位置$R$が求まります。

回転

　オブジェクトの正面を示すベクトルと上方を示すベクトルから、Quaternion.LookRotationによってオブジェクトの回転を表すクォータニオンを計算することができます。つまり、鏡面で反転させた二つのベクトルを求めることで鏡面位置における回転を計算できます。鏡面反転座標ベクトルを求める式は座標を求める式とほぼ同じですが、座標ではなくベクトルなので平面及びベクトルを原点$O$に移動し計算します。よって、$P=(0, 0, 0)$となります。

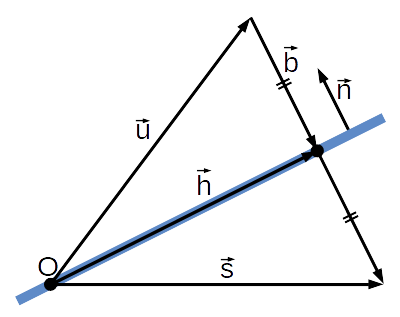図2. 鏡面における任意のベクトル$\vec{u}$と鏡面反転したベクトル$\vec{s}$の関係

$\vec{b}$及び $\vec{s}$は

$$ \vec{b}=\vec{h}-\vec{u},\quad \vec{s}=\vec{h}+\vec{b}\\　\tag{7} $$

なので、$\vec{s}$は

$$ \vec{s}=2\vec{h}-\vec{u}　\tag{8} $$

となります。ベクトル方程式は式$(2)$と同様に

$$ \begin{align} \left\{ \begin{array}{l} x&=u_{x}+n_{x}t\\ y&=u_{y}+n_{y}t\\ z&=u_{z}+n_{z}t \end{array} \right.　\tag{9} \end{align} $$

また、式$(6)$より

$$ t=-\vec{n}\cdot \vec{u} \tag{10} $$

となります。この$t$を式$(9)$に代入することで、$\vec{h}$が求まります。よって、式$(8)$より鏡面で反転したベクトルを求めることができます。

Script

　作成したScriptは以下の通りです。先ほど求めた式より反射用カメラの位置と回転を求めています。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class PlanarReflectionCubemap : MonoBehaviour
{
    private Transform trf_camera_main, trf_camera_reflection;
    private RenderTexture renderTex_reflection;
    private Cubemap cubemap_reflection;
    private GameObject obj_reflection_camera;
    private Camera camera_main, camera_reflection;
    private Material mat_refPlane;
    private int property_id_cubemap;

    private Matrix4x4 matrix_proj;

    // Start is called before the first frame update
    void Start()
    {
        renderTex_reflection = new RenderTexture(512, 512, 24, RenderTextureFormat.ARGB32);
        renderTex_reflection.dimension = UnityEngine.Rendering.TextureDimension.Cube;

        camera_main = Camera.main;
        trf_camera_main = Camera.main.transform;

        obj_reflection_camera = new GameObject();
        obj_reflection_camera.name = "Reflection Camera";
        camera_reflection = obj_reflection_camera.AddComponent();
        camera_reflection.cullingMask &= ~(1 << LayerMask.NameToLayer("Mirror"));
        camera_reflection.enabled = false;
        camera_reflection.useOcclusionCulling = false;

        trf_camera_reflection = obj_reflection_camera.transform;
        trf_camera_reflection.position = CalculateMirrorPosition(transform.up, transform.position, trf_camera_main.position);
        Vector3 v3_forward = CalCalculateMirrorVector(transform.up, trf_camera_main.forward);
        Vector3 v3_up = CalCalculateMirrorVector(transform.up, trf_camera_main.up);
        trf_camera_reflection.rotation = Quaternion.LookRotation(v3_forward, v3_up);

        property_id_cubemap = Shader.PropertyToID("_Cubemap");

        mat_refPlane = gameObject.GetComponent().sharedMaterial;
        mat_refPlane.SetTexture(property_id_cubemap, renderTex_reflection);
    }

    private void SetReflectionCamera()
    {
        Vector3 normal = transform.up;
        Vector3 pos = transform.position;

        trf_camera_reflection.position = CalculateMirrorPosition(normal, pos, trf_camera_main.position);
        Vector3 v3_forward = CalCalculateMirrorVector(normal, trf_camera_main.forward);
        Vector3 v3_up = CalCalculateMirrorVector(normal, trf_camera_main.up);
        trf_camera_reflection.rotation = Quaternion.LookRotation(v3_forward, v3_up);
    }

    void OnWillRenderObject()
    {
        SetReflectionCamera();
        GL.invertCulling = true;
        camera_reflection.RenderToCubemap(renderTex_reflection);
        GL.invertCulling = false;
        mat_refPlane.SetTexture(property_id_cubemap, renderTex_reflection);
    }

    Vector3 CalculateMirrorPosition(Vector3 v3_normal, Vector3 v3_plane_pos, Vector3 v3_camera_pos)
    {
        v3_normal = Vector3.Normalize(v3_normal);
        float t = Vector3.Dot(v3_normal, v3_plane_pos) - Vector3.Dot(v3_normal, v3_camera_pos);
        Vector3 v3_intersection = new Vector3(v3_camera_pos.x + v3_normal.x * t, v3_camera_pos.y + v3_normal.y * t, v3_camera_pos.z + v3_normal.z * t);

        return v3_intersection * 2.0f - v3_camera_pos;
    }

    Vector3 CalCalculateMirrorVector(Vector3 v3_normal, Vector3 v3_dir)
    {
        v3_normal = Vector3.Normalize(v3_normal);
        float t = -Vector3.Dot(v3_normal, v3_dir);
        Vector3 v3_intersection = new Vector3(v3_dir.x + v3_normal.x * t, v3_dir.y + v3_normal.y * t, v3_dir.z + v3_normal.z * t);

        return v3_intersection * 2.0f - v3_dir;
    }
}

Shader

　Cubemapを表示するだけのシェーダーです。

Shader "Unlit/CubeMap"
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
		_Cubemap ("Cubemap", CUBE) = "" {}
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }

        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
				float3 normal : NORMAL;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 vertex : SV_POSITION;
				float3 normal : NORMAL;
				float3 worldPos : TEXCOORD1;
            };

            sampler2D _MainTex;
            float4 _MainTex_ST;

			samplerCUBE _Cubemap;

            v2f vert (appdata v)
            {
                v2f o;
				float4 vt = v.vertex;
                o.vertex = UnityObjectToClipPos(vt);
                o.uv = TRANSFORM_TEX(v.uv, _MainTex);
				o.normal = UnityObjectToWorldNormal(v.normal);
				o.worldPos = mul(unity_ObjectToWorld, vt).xyz;

                return o;
            }

            fixed4 frag (v2f i) : SV_Target
            {
				float3 normal = normalize(i.normal);
				float3 viewDir = normalize(_WorldSpaceCameraPos - i.worldPos);
				float3 reflectDir = reflect(-viewDir, normal);

                fixed4 col = texCUBE(_Cubemap, reflectDir);
				col.a = 1.0;
                return col;
            }
            ENDCG
        }
    }
}

実行結果

　上記Scriptの実行結果は以下の通りです。Cubemapによる平面の鏡面反射が描画できました。しかし、CalculateObliqueMatrixによってクリップ平面を変更すると正しい結果が得られませんでした。

RenderTextureに変更

　以上で説明した方法を用いて、以前の記事（平面の鏡面反射）で行っていたように鏡面の画像をRenderTextureで取得するように変更してみました。

Script

　作成したScriptは以下の通りです。CalculateObliqueMatrixによって得られるprojection matrixでは画像が反転してしまうので、Matrix4x4.Scaleによって反転しています。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class PlanarReflectionTrf : MonoBehaviour
{
    private Transform trf_camera_main, trf_camera_reflection;
    private RenderTexture renderTex_reflection;
    private GameObject obj_reflection_camera;
    private Camera camera_main, camera_reflection;
    private Material mat_refPlane;
    private int property_id_refTex;

    private Matrix4x4 matrix_proj;

    // Start is called before the first frame update
    void Start()
    {
        renderTex_reflection = new RenderTexture(Screen.width, Screen.height, 0, RenderTextureFormat.ARGB32);

        camera_main = Camera.main;
        trf_camera_main = Camera.main.transform;

        obj_reflection_camera = new GameObject();
        obj_reflection_camera.name = "Reflection Camera";
        camera_reflection = obj_reflection_camera.AddComponent();
        camera_reflection.cullingMask &= ~(1 << LayerMask.NameToLayer("Mirror"));
        camera_reflection.enabled = false;
        camera_reflection.useOcclusionCulling = false;
        camera_reflection.targetTexture = renderTex_reflection;

        trf_camera_reflection = obj_reflection_camera.transform;
        trf_camera_reflection.position = CalculateMirrorPosition(transform.up, transform.position, trf_camera_main.position);
        Vector3 v3_forward = CalCalculateMirrorVector(transform.up, trf_camera_main.forward);
        Vector3 v3_up = CalCalculateMirrorVector(transform.up, trf_camera_main.up);
        trf_camera_reflection.rotation = Quaternion.LookRotation(v3_forward, v3_up);

        property_id_refTex = Shader.PropertyToID("_ReflectionTex");

        mat_refPlane = gameObject.GetComponent().sharedMaterial;
        mat_refPlane.SetTexture(property_id_refTex, renderTex_reflection);
    }

    private void SetReflectionCamera()
    {
        Vector3 normal = transform.up;
        Vector3 pos = transform.position;

        trf_camera_reflection.position = CalculateMirrorPosition(normal, pos, trf_camera_main.position);
        Vector3 v3_forward = CalCalculateMirrorVector(normal, trf_camera_main.forward);
        Vector3 v3_up = CalCalculateMirrorVector(normal, trf_camera_main.up);
        trf_camera_reflection.rotation = Quaternion.LookRotation(v3_forward, v3_up);

        Matrix4x4 mainCamMatrix = camera_main.worldToCameraMatrix;

        Vector3 cpos = camera_reflection.worldToCameraMatrix.MultiplyPoint(pos);

        Vector3 cnormal = camera_reflection.worldToCameraMatrix.MultiplyVector(normal).normalized;

        Vector4 clipPlane = new Vector4(cnormal.x, cnormal.y, cnormal.z, -Vector3.Dot(cpos, cnormal));

        camera_reflection.projectionMatrix = Matrix4x4.Scale(new Vector3(-1.0f, 1.0f, 1.0f)) * camera_main.CalculateObliqueMatrix(clipPlane);
    }

    void OnWillRenderObject()
    {
        SetReflectionCamera();
        GL.invertCulling = true;
        camera_reflection.Render();
        GL.invertCulling = false;
        mat_refPlane.SetTexture(property_id_refTex, renderTex_reflection);
    }

    Vector3 CalculateMirrorPosition(Vector3 v3_normal, Vector3 v3_plane_pos, Vector3 v3_camera_pos)
    {
        v3_normal = Vector3.Normalize(v3_normal);
        float t = Vector3.Dot(v3_normal, v3_plane_pos) - Vector3.Dot(v3_normal, v3_camera_pos);
        Vector3 v3_intersection = new Vector3(v3_camera_pos.x + v3_normal.x * t, v3_camera_pos.y + v3_normal.y * t, v3_camera_pos.z + v3_normal.z * t);

        return v3_intersection + v3_intersection - v3_camera_pos;
    }

    Vector3 CalCalculateMirrorVector(Vector3 v3_normal, Vector3 v3_dir)
    {
        v3_normal = Vector3.Normalize(v3_normal);
        float t = -Vector3.Dot(v3_normal, v3_dir);
        Vector3 v3_intersection = new Vector3(v3_dir.x + v3_normal.x * t, v3_dir.y + v3_normal.y * t, v3_dir.z + v3_normal.z * t);

        return v3_intersection * 2.0f - v3_dir;
    }
}