シェーダでノイズ2（パーリンノイズ）

2019.02.16
Unity
shader, script, noise

　パーリンノイズは単純なランダムノイズと異なり、滑らかなノイズが得られます。そのため、様々なテクスチャの生成や炎、雲及び地形などの自然物を表現する際によく使用されます。

1. 一次元パーリンノイズ
- 1.1. Script
- 1.2. 実行結果
2. 二次元パーリンノイズ
- 2.1. shader
- 2.2. 実行結果
3. 参考サイト

一次元パーリンノイズ

　始めに、xの少数部分を取り出します。これにより、整数の間で$0$から$1$未満の値を繰り返すようになります。したがって、下図で色分けされているように整数の間を一つの区間として区切ることができます。ここで、区切られた区間を格子、区間の境目を格子線とします。また、丸で囲まれている座標を格子点とします。

ある格子内において、左側の格子点、つまり、$floor(x)$におけるランダムな値$a_{L}$と右側の格子点 $floor(x+1)$におけるランダムな値$a_{R}$ を求めます。次に、それぞれの格子点を原点とし、ランダムな値を傾きとする直線を以下の式より求めます。

$$ \begin{align} &w_{L}(x)=a_{L}\cdot frac(x)\\ &w_{R}(x)=a_{R}\cdot (frac(x)-1) \end{align} $$

上式により求められる直線は下図のようになります。赤色の直線が$w_{L}(x)$、青色の直線が$w_{R}(x)$です。ある格子線の左側の青い直線と右側の赤い直線が一直線となっているのは、傾きとして求められるランダムな値が同じ格子点であれば、必ず同じ値となるためです。

この直線により求められる二つの値をエルミート補間することでノイズが求まります。使用するエルミート補間の式は以下の通りです。

$$ u=3f^2-2f^3 $$

また、エルミート補間を図にすると以下のようになります。

よって、ノイズを求める式は以下の式となります。

$$ \begin{align} &f=frac(x),u=f^{2}(3-2f)\\ &n=lerp(w_{L},w_{R},u) \end{align} $$

この式より、以下の図に示すノイズを求めることができます。

上図より、滑らかでかつランダムな値が得られることがわかります。また、パーリンノイズは格子線上において必ず$0$となることもわかります。

Script

　Unityで一次元パーリンノイズを求めるスクリプトを作成しました。スクリプトは以下の通りです。このスクリプトは適当なゲームオブジェクトにアタッチすれば動作します。このスクリプトでは、上記のように直線をエルミート補間する方法だけではなく、こちらに掲載されているウェーブレット関数を求め、それらを線形補間する方法でもノイズを計算しています。


using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEngine.UI;

public class PerlinNoise : MonoBehaviour {

    public Sprite sprite_UISprite, sprite_checkmark, sprite_knob, sprite_background;
    public Material mat_default_line;
    private GameObject obj_line, obj_graph, obj_canvas, obj_grad, obj_wave;
    private RectTransform[] rect_scale = new RectTransform[5];
    private RectTransform[] rect_image = new RectTransform[2];
    private Toggle[] toggle = new Toggle[4];
    private Slider slider_seed, slider_width, slider_height, slider_scale;
    private LineRenderer line_easeNoize, line_waveNoize, line_frame, line_center;
    private LineRenderer[] line_x = new LineRenderer[9];
    private LineRenderer[] line_y = new LineRenderer[8];
    private LineRenderer[] line_grad = new LineRenderer[20];
    private LineRenderer[] line_wave = new LineRenderer[2];
    private int step = 20, range = 10, linerenderer_size;
    private float scale = 1f;
    private Vector2 graph_size = new Vector2(10.5f, 2.8f);
    private Vector2[] text_offset = { new Vector2(-5f, 0f), new Vector2(0f, -5f) };
    private Vector2 screenSize;
    private Text[] text_scale = new Text[2];
    private Color color_bg = new Color(0.745f, 0.745f, 0.745f, 1);

    // Use this for initialization
    void Start() {
        screenSize = new Vector2(Screen.width, Screen.height);
        CameraPosition();

        //カメラ
        Camera.main.orthographic = true;
        Camera.main.orthographicSize = 4f;
        Camera.main.clearFlags = CameraClearFlags.SolidColor;
        Camera.main.backgroundColor = color_bg;

        //UIの作成
        obj_canvas = GameObject.Find("Canvas");
        if (obj_canvas == null)
        {
            obj_canvas = AddCanvas();
        }

        GameObject obj_ui = new GameObject("UI");
        obj_ui.transform.SetParent(obj_canvas.transform);
        obj_ui.layer = LayerMask.NameToLayer("UI");
        RectTransform rect_ui = obj_ui.AddComponent();
        rect_ui.anchoredPosition = Vector2.zero;
        rect_ui.anchorMin = new Vector2(0f, 1f);
        rect_ui.anchorMax = new Vector2(0f, 1f);

        //toggle
        toggle[0] = AddToggle(obj_ui, new Vector2(90f, -20f), "toggle", "hermite");
        toggle[1] = AddToggle(obj_ui, new Vector2(170f, -20), "toggle", "L(x)");
        toggle[2] = AddToggle(obj_ui, new Vector2(90f, -45f), "toggle", "wavelet");
        toggle[3] = AddToggle(obj_ui, new Vector2(170f, -45f), "toggle", "W(x)");

        toggle[0].isOn = true;
        toggle[3].interactable = false;

        //slider
        slider_seed = AddSlider(obj_ui, new Vector2(245f, -20f), "slider");
        slider_seed.wholeNumbers = true;
        slider_seed.maxValue = 300;
        Text text_slider = AddText(obj_ui, new Vector2(235f, -20f), 16, "Seed", "text_seed").GetComponent();
        text_slider.alignment = TextAnchor.MiddleLeft;

        slider_width = AddSlider(obj_ui, new Vector2(410f, -20f), "slider_width");
        slider_width.minValue = 1f;
        slider_width.maxValue = 20f;
        slider_width.value = graph_size.x;
        Text text_width = AddText(obj_ui, new Vector2(390f, -20f), 16, "width", "text_width").GetComponent();
        text_width.alignment = TextAnchor.MiddleLeft;

        slider_height = AddSlider(obj_ui, new Vector2(410f, -40f), "slider_height");
        slider_height.minValue = 0.5f;
        slider_height.maxValue = 5f;
        slider_height.value = graph_size.y;
        Text text_height = AddText(obj_ui, new Vector2(390f, -40f), 16, "height", "text_height").GetComponent();
        text_height.alignment = TextAnchor.MiddleLeft;

        slider_scale = AddSlider(obj_ui, new Vector2(245f, -40f), "slider_scale");
        slider_scale.minValue = 0;
        slider_scale.maxValue = 2;
        slider_scale.wholeNumbers = true;
        slider_scale.value = 1;
        Text text_yscale = AddText(obj_ui, new Vector2(235f, -40f), 16, "y", "text_scale").GetComponent();
        text_yscale.alignment = TextAnchor.MiddleLeft;

        //目盛り
        string[] str = { "-1", "0", "1", "0", "10" };
        for (int i = 0; i < 5; i++)
        {
            GameObject obj_scale_text = AddText(obj_canvas, Vector2.zero, 18, str[i], str[i]);
            Text text_n = obj_scale_text.GetComponent();
            if (i == 0) text_scale[0] = text_n;
            if (i == 2) text_scale[1] = text_n;

            rect_scale[i] = obj_scale_text.GetComponent();
            rect_scale[i].anchorMin = Vector2.zero;
            rect_scale[i].anchorMax = Vector2.zero;

            if (i < 3)
            {
                rect_scale[i].pivot = new Vector2(1f, 0.5f);
                text_n.alignment = TextAnchor.MiddleRight;
            }
            else
            {
                rect_scale[i].pivot = new Vector2(0.5f, 1f);
                text_n.alignment = TextAnchor.UpperCenter;
            }
        }
        ScaleText();

        //枠線
        obj_graph = new GameObject("graph");
        obj_line = new GameObject("frame");
        obj_line.transform.position = Vector3.zero;
        line_frame = obj_line.AddComponent();
#if UNITY_EDITOR
        line_frame.material = UnityEditor.AssetDatabase.GetBuiltinExtraResource("Default-Line.mat");
#else
            line_frame.material = mat_default_line;
#endif

        line_frame.startColor = Color.black;
        line_frame.endColor = Color.black;
        line_frame.startWidth = 0.05f;
        line_frame.endWidth = 0.05f;
        line_frame.positionCount = 5;

        linerenderer_size = range * step;

        //中心線
        line_center = LineCreator(obj_line, obj_graph, "center", Vector3.zero, Color.black, 0.05f, 2);

        //縦線
        for (int n = 0; n < line_x.Length; n++)
        {
            line_x[n] = LineCreator(obj_line, obj_graph, "v_line", Vector3.zero, new Color(0.67f, 0.67f, 0.67f, 1f), 0.03f, 2);
        }

        //横線
        for (int n = 0; n < line_y.Length * 0.5f; n++)
        {
            line_y[n] = LineCreator(obj_line, obj_graph, "h_line", Vector3.zero, new Color(0.67f, 0.67f, 0.67f, 1f), 0.03f, 2);
            line_y[line_y.Length - n - 1] = LineCreator(obj_line, obj_graph, "h_line", Vector3.zero, new Color(0.67f, 0.67f, 0.67f, 1f), 0.02f, 2);
        }

        //ノイズ用ラインレンダラー
        line_easeNoize = LineCreator(obj_line, null, "Noise-Ease", Vector3.zero, new Color(1f, 0, 1f, 1f), 0.05f, linerenderer_size + 1);
        line_waveNoize = LineCreator(obj_line, null, "Noise-Wavelet", Vector3.zero, new Color(1f, 0, 1f, 1f), 0.05f, linerenderer_size + 1);

        //L(x)
        obj_grad = new GameObject("L(t)");
        for (int x = 0; x < range; x++)
        {
            line_grad[x] = LineCreator(obj_line, obj_grad, "grad_left_" + x.ToString(), Vector3.zero, Color.red, 0.05f, 2);
            line_grad[x + range] = LineCreator(obj_line, obj_grad, "grad_right_" + x.ToString(), Vector3.zero, Color.blue, 0.05f, 2);
        }

        //wavelet用ラインレンダラー
        obj_wave = new GameObject();
        line_wave[0] = LineCreator(obj_line, obj_wave, "wavelet_left", Vector3.zero, Color.red, 0.05f, linerenderer_size + 1);
        line_wave[1] = LineCreator(obj_line, obj_wave, "wavelet_right", Vector3.zero, Color.blue, 0.05f, linerenderer_size + 1);


        line_waveNoize.gameObject.SetActive(false);
        obj_grad.SetActive(false);
        obj_wave.SetActive(false);

        SetUI();
        GraphLine();
        DrawNoize(0);
    }

    //グラフの枠線とグリッド線
    void GraphLine()
    {
        //枠線
        line_frame.SetPosition(0, new Vector3(0, graph_size.y, -1f));
        line_frame.SetPosition(1, new Vector3(0, -graph_size.y, -1f));
        line_frame.SetPosition(2, new Vector3(graph_size.x, -graph_size.y, -1f));
        line_frame.SetPosition(3, new Vector3(graph_size.x, graph_size.y, -1f));
        line_frame.SetPosition(4, new Vector3(0, graph_size.y, -1f));

        //中心線
        line_center.SetPosition(0, new Vector3(0, 0, 1f));
        line_center.SetPosition(1, new Vector3(graph_size.x, 0, 1f));

        //縦線
        float x = graph_size.x / range;
        float y = -graph_size.y;
        for (int n = 0; n < line_x.Length; n++)
        {
            for (int m = 0; m < 2; m++)
            {
                y *= -1;
                line_x[n].SetPosition(m, new Vector3((n + 1f) * x, y, 2f));
            }
        }

        //横線
        y = graph_size.y / 5f;
        for (int n = 0; n < line_y.Length * 0.5f; n++)
        {
            for (int m = 0; m < 2; m++)
            {
                line_y[n].SetPosition(m, new Vector3(m * graph_size.x, y * (n + 1), 2f));
                line_y[line_y.Length - n - 1].SetPosition(m, new Vector3(m * graph_size.x, -y * (n + 1), 2f));
            }
        }


    }

    //UI要素の動作
    void SetUI()
    {
        //toggle
        toggle[0].onValueChanged.AddListener((flg) => {
            if (toggle[0].isOn)
            {
                line_easeNoize.gameObject.SetActive(true);
                line_waveNoize.gameObject.SetActive(false);
                toggle[1].interactable = true;
                toggle[2].isOn = false;
                toggle[3].isOn = false;
                toggle[3].interactable = false;
            }
            else
            {
                line_easeNoize.gameObject.SetActive(false);
            }
        });

        toggle[2].onValueChanged.AddListener((flg) => {
            if (toggle[2].isOn)
            {
                line_waveNoize.gameObject.SetActive(true);
                line_easeNoize.gameObject.SetActive(false);
                toggle[0].isOn = false;
                toggle[1].isOn = false;
                toggle[1].interactable = false;
                toggle[3].interactable = true;
            }
            else
            {
                line_waveNoize.gameObject.SetActive(false);
            }
        });

        toggle[1].onValueChanged.AddListener((flg) => {
            if (toggle[1].isOn)
            {
                obj_grad.SetActive(true);
            }
            else
            {
                obj_grad.SetActive(false);
            }
        });

        toggle[3].onValueChanged.AddListener((flg) => {
            if (toggle[3].isOn)
            {
                obj_wave.SetActive(true);
            }
            else
            {
                obj_wave.SetActive(false);
            }
        });

        //slider
        slider_seed.onValueChanged.AddListener((flg) =>
        {
            DrawNoize((int)slider_seed.value);
        });

        slider_width.onValueChanged.AddListener((flg) =>
        {
            graph_size.x = slider_width.value;
            GraphLine();
            DrawNoize((int)slider_seed.value);
            CameraPosition();
            ScaleText();
        });

        slider_height.onValueChanged.AddListener((flg) =>
        {
            graph_size.y = slider_height.value;
            GraphLine();
            DrawNoize((int)slider_seed.value);
            ScaleText();
        });

        slider_scale.onValueChanged.AddListener((flg) =>
        {
            int val = (int)slider_scale.value;
            switch (val)
            {
                case 0:
                    text_scale[0].text = "-0.5";
                    text_scale[1].text = "0.5";
                    scale = 2f;
                    break;

                case 1:
                    text_scale[0].text = "-1";
                    text_scale[1].text = "1";
                    scale = 1f;
                    break;

                case 2:
                    text_scale[0].text = "-2";
                    text_scale[1].text = "2";
                    scale = 0.5f;
                    break;

                default:
                    break;
            }
            DrawNoize((int)slider_seed.value);
        });
    }

    //目盛りの位置
    void ScaleText()
    {
        Vector2[] text_wpos = new Vector2[5];
        text_wpos[0] = RectTransformUtility.WorldToScreenPoint(Camera.main, new Vector3(0f, -graph_size.y, 0f));
        text_wpos[1] = RectTransformUtility.WorldToScreenPoint(Camera.main, new Vector3(0f, 0f, 0f));
        text_wpos[2] = RectTransformUtility.WorldToScreenPoint(Camera.main, new Vector3(0f, graph_size.y, 0f));
        text_wpos[3] = RectTransformUtility.WorldToScreenPoint(Camera.main, new Vector3(0f, -graph_size.y, 0f));
        text_wpos[4] = RectTransformUtility.WorldToScreenPoint(Camera.main, new Vector3(graph_size.x, -graph_size.y, 0f));

        for (int i = 0; i < 5; i++)
        {
            if (i < 3)
            {
                rect_scale[i].position = text_wpos[i] + text_offset[0];
            }
            else
            {
                rect_scale[i].position = text_wpos[i] + text_offset[1];
            }
        }
    }

    //LineRendererの作成
    LineRenderer LineCreator(GameObject obj, GameObject obj_parent, string line_name, Vector3 pos, Color color, float width, int posSize)
    {
        GameObject obj_tmp = Instantiate(obj, pos, Quaternion.identity);
        if(obj_parent != null) obj_tmp.transform.SetParent(obj_parent.transform);
        obj_tmp.name = line_name;
        LineRenderer line = obj_tmp.GetComponent();

        line.startColor = color;
        line.endColor = color;
        line.startWidth = width;
        line.endWidth = width;

        line.positionCount = posSize;

        return line;
    }

    //Canvas
    GameObject AddCanvas()
    {
        GameObject obj = new GameObject("Canvas");
        obj.layer = LayerMask.NameToLayer("UI");
        Canvas canvas = obj.AddComponent

実行結果

　トグルを操作することで表示するグラフを変更できます。hermiteが直線をエルミート補間する方法で求められるノイズを、$L(x)$はノイズを求めるときに使用した直線を表示します。また、waveletはウェーブレット関数を線形補間することで求められるノイズを、$W(x)$はウェーブレット関数を表示します。

二次元パーリンノイズ

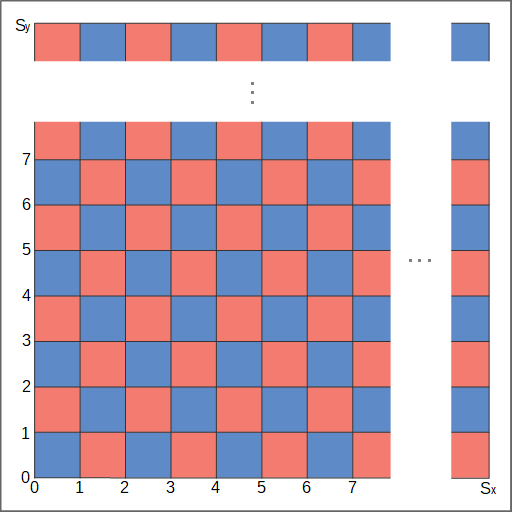
　二次元パーリンノイズは一次元の時と同様にして求めることができます。初めに、$x$及び$y$の少数部分を取り出すことで、下図に示すように格子状に区切ります。

一次元の場合は直線を補間しノイズを求めましたが、二次元の場合は平面を補間することでノイズを求めます。平面の式は以下の通りです。

$$ \begin{align} w(x,y)&=a_{x}\cdot x+a_{y}\cdot y\\ &=(a_{x},a_{y})\cdot (x,y) \end{align} $$

$a_{x}$及び$a_{y}$はそれぞれランダムな値を示しています。平面の方程式は上式のように、ランダムな値のベクトルと格子点から格子内にある任意の点に向かうベクトルの内積で表すことができます。よって、ランダムな値で構成されるグラディエントと距離ベクトルの内積を格子点ごとに求め、それらを補間することでノイズが求まることがわかります。この式を用いて、ある点$P$における値を求めます。下図は点$P$のある格子を示しています。

先ほどの式より格子点ごとに$w$を求めます。それぞれの格子点から点$P$へ向かう距離ベクトルは以下の式で表されます。

$$ \begin{align} &\vec{d_{00}}=(frac(x),frac(y))\\ &\vec{d_{10}}=(frac(x)-1,frac(y))\\ &\vec{d_{01}}=(frac(x),frac(y)-1)\\ &\vec{d_{11}}=(frac(x)-1,frac(y)-1)\\ \end{align} $$

これより、格子点ごとの$w$ は以下のようになります。

$$ \begin{align} &w_{00}(x,y)=(a_{00x},a_{00y})\cdot (frac(x),frac(y))\\ &w_{10}(x,y)=(a_{10x},a_{10y})\cdot (frac(x)-1,frac(y))\\ &w_{01}(x,y)=(a_{01x},a_{01y})\cdot (frac(x),frac(y)-1)\\ &w_{11}(x,y)=(a_{11x},a_{11y})\cdot (frac(x)-1,frac(y)-1)\\ \end{align} $$

この式より求められる値をエルミート補間することでノイズが求まります。よって、ノイズは以下の式より求めることができます。

$$ \begin{align} &f_{x}=frac(x),f_{y}=frac(y)\\ &u_{x}=3f_{x}^{2}-2f_{x}^{3},u_{y}=3f_{y}^{2}-2f_{y}^3\\ &n=lerp\{lerp(w_{00},w_{10},u_{x}),lerp(w_{01},w_{11},u_{x}),u_{y}\} \end{align} $$

shader

　二次元パーリンノイズのシェーダを以下に示します。uv座標に定数を掛けることにより格子数を決定しています。

Shader "Noise/PerlinNoise"
{
	Properties
	{
		_MainTex ("Texture", 2D) = "white" {}
		_Seed ("SeedX", Int) = 0
		_SizeX ("SizeX", Int) = 1
		_SizeY ("SizeY", Int) = 1
	}
	SubShader
	{
		Tags { "RenderType"="Opaque" }

		Pass
		{
			CGPROGRAM
			#pragma vertex vert
			#pragma fragment frag
			
			#include "UnityCG.cginc"

			struct appdata
			{
				float4 vertex : POSITION;
				float2 uv : TEXCOORD0;
			};

			struct v2f
			{
				float2 uv : TEXCOORD0;
				float4 vertex : SV_POSITION;
			};

			sampler2D _MainTex;
			float4 _MainTex_ST;
			
			int _Seed;
			int _SizeX;
			int _SizeY;
			
			float2 rand(float2 st, int seed)
			{
				float2 s = float2(dot(st, float2(127.1, 311.7)) + seed, dot(st, float2(269.5, 183.3)) + seed);
				return -1 + 2 * frac(sin(s) * 43758.5453123);
			}

			float noise(float2 st, int seed)
			{
				float2 p = floor(st);
				float2 f = frac(st);

				float w00 = dot(rand(p, seed), f);
				float w10 = dot(rand(p + float2(1, 0), seed), f - float2(1, 0));
				float w01 = dot(rand(p + float2(0, 1), seed), f - float2(0, 1));
				float w11 = dot(rand(p + float2(1, 1), seed), f - float2(1, 1));
				
				float2 u = f * f * (3 - 2 * f);

				return lerp(lerp(w00, w10, u.x), lerp(w01, w11, u.x), u.y);
			}

			v2f vert (appdata v)
			{
				v2f o;
				o.vertex = UnityObjectToClipPos(v.vertex);
				o.uv = TRANSFORM_TEX(v.uv, _MainTex);
				return o;
			}
			
			fixed4 frag (v2f i) : SV_Target
			{
				fixed4 col;
				col.rgb = noise(float2(i.uv.x * _SizeX, i.uv.y * _SizeY), _Seed) * 0.5 + 0.5;
				col.a = 1;
				return col;
			}
			ENDCG
		}
	}
}