空の色（大気散乱シミュレーション）

2019.09.16
Unity
shader

　太陽光が大気へ突入すると散乱が起こります。この散乱をシェーダーでシミュレーションすることで、空の色を描画することができます。この記事では、GPU Gems 2：Chapter 16. Accurate Atmospheric Scatteringを参考にシェーダーを作成しました。

1. シェーダーの作成
- 1.1. shader
- 1.2. 実行結果
2. シェーダーの変更
- 2.1. 実行結果
3. Skyboxでの使用
- 3.1. shader
- 3.2. 実行結果
4. 参考サイト

シェーダーの作成

shader

　作成したシェーダーは以下の通りです。GPU Gem2のコードから大きな変更はありません。

Shader "Sky/Sky_Rayleigh"
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
		_InnerRadius("InnerRadius", Float) = 10000
		_OuterRadius("OuterRadius", Float) = 10250
		_Kr("RayleighScatteringCoefficient", Float) = 0.0025
		_Km("MieScatteringCoefficient", Float) = 0.001
    }
    SubShader
    {
		Tags { "RenderType"="Background" "Queue"="Background" }

        Pass
        {
			Tags { "LightMode"="ForwardBase" }

			Cull Off

			CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

			#define PI 3.14159265359

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 vertex : SV_POSITION;
				float3 worldPos :TEXCOORD1;
            };

            sampler2D _MainTex;
            float4 _MainTex_ST;
			
			float _InnerRadius;
			float _OuterRadius;

			float _Kr;
			float _Km;

			static const float fSamples = 2.0;

			static const float3 three_primary_colors = float3(0.68, 0.55, 0.44);
			static const float3 v3InvWaveLength = 1.0 / pow(three_primary_colors, 4.0);

			static const float fOuterRadius = _OuterRadius;
			static const float fInnerRadius = _InnerRadius;

			static const float fESun = 20.0;
			static const float fKrESun = _Kr * fESun;
			static const float fKmESun = _Km * fESun;

			static const float fKr4PI = _Kr * 4.0 * PI;
			static const float fKm4PI = _Km * 4.0 * PI;

			static const float fScale = 1.0 / (_OuterRadius - _InnerRadius);;
			static const float fScaleDepth = 0.25;
			static const float fScaleOverScaleDepth = fScale / fScaleDepth;

			static const float g = -0.999f;
			static const float g2 = g * g;

            v2f vert (appdata v)
            {
                v2f o;
				float4 vt = v.vertex;
                o.vertex = UnityObjectToClipPos(vt);
                o.uv = TRANSFORM_TEX(v.uv, _MainTex);
				o.worldPos = mul(unity_ObjectToWorld, vt).xyz;
                return o;
            }

			float Scale(float fcos){
				float x = 1.0 - fcos;
				return fScaleDepth * exp(-0.00287 + x * (0.459 + x * (3.83 + x * (-6.8 + x * 5.25))));
			}

            fixed4 frag (v2f i) : SV_Target
            {
				float3 worldPos = i.worldPos;
				float3 v3CameraPos = _WorldSpaceCameraPos;
				v3CameraPos.y = fInnerRadius;
				float3 v3LightDir = normalize(UnityWorldSpaceLightDir(worldPos));

				float3 v3Ray = worldPos - v3CameraPos;
				float fFar = length(v3Ray);
				v3Ray /= fFar;

				float3 v3Start = v3CameraPos;
				float fCameraHeight = length(v3CameraPos);
				float fStartAngle = dot(v3Ray, v3Start) / fCameraHeight;
				float fStartDepth = exp(fScaleOverScaleDepth * (fInnerRadius - fCameraHeight));
				float fStartOffset = fStartDepth * Scale(fStartAngle);

				float fSampleLength = fFar / fSamples;
				float fScaledLength = fSampleLength * fScale;
				float3 v3SampleRay = v3Ray * fSampleLength;
				float3 v3SamplePoint = v3Start + v3SampleRay * 0.5;

				float3 v3FrontColor = 0.0;
				for(int n = 0; n < int(fSamples); n++){
					float fHeight = length(v3SamplePoint);
					float fDepth = exp(fScaleOverScaleDepth * (fInnerRadius - fHeight));
					float fLightAngle = dot(v3LightDir, v3SamplePoint) / fHeight;
					float fCameraAngle = dot(v3Ray, v3SamplePoint) / fHeight;
					float fScatter = (fStartOffset + fDepth * (Scale(fLightAngle) - Scale(fCameraAngle)));
					float3 v3Attenuate = exp(-fScatter * (v3InvWaveLength * fKr4PI + fKm4PI));
					v3FrontColor += v3Attenuate * (fDepth * fScaledLength);
					v3SamplePoint += v3SampleRay;
				}

				float3 c0 = v3FrontColor * (v3InvWaveLength * fKrESun);
				float3 c1 = v3FrontColor * fKmESun;
				float3 v3Direction = v3CameraPos - worldPos;

				float fcos = dot(v3LightDir, v3Direction) / length(v3Direction);
				float fcos2 = fcos * fcos;

				float rayleighPhase = 0.75 * (1.0 + fcos2);
				float miePhase = 1.5 * ((1.0 - g2) / (2.0 + g2)) * (1.0 + fcos2) / pow(1.0 + g2 - 2.0 * g * fcos, 1.5);

				fixed4 col = 1.0;
				col.rgb = rayleighPhase * c0 + miePhase * c1;
                return col;
            }
            ENDCG
        }
    }
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

Shader "Sky/Sky_Rayleigh"

{

Properties

{

_MainTex ("Texture", 2D) = "white" {}

_InnerRadius("InnerRadius", Float) = 10000

_OuterRadius("OuterRadius", Float) = 10250

_Kr("RayleighScatteringCoefficient", Float) = 0.0025

_Km("MieScatteringCoefficient", Float) = 0.001

}

SubShader

{

Tags { "RenderType"="Background" "Queue"="Background" }

Pass

{

Tags { "LightMode"="ForwardBase" }

Cull Off

CGPROGRAM

#pragma vertex vert

#pragma fragment frag

#include "UnityCG.cginc"

#define PI 3.14159265359

struct appdata

{

float4 vertex : POSITION;

float2 uv : TEXCOORD0;

};

struct v2f

{

float2 uv : TEXCOORD0;

float4 vertex : SV_POSITION;

float3 worldPos :TEXCOORD1;

};

sampler2D _MainTex;

float4 _MainTex_ST;

float _InnerRadius;

float _OuterRadius;

float _Kr;

float _Km;

static const float fSamples = 2.0;

static const float3 three_primary_colors = float3(0.68, 0.55, 0.44);

static const float3 v3InvWaveLength = 1.0 / pow(three_primary_colors, 4.0);

static const float fOuterRadius = _OuterRadius;

static const float fInnerRadius = _InnerRadius;

static const float fESun = 20.0;

static const float fKrESun = _Kr * fESun;

static const float fKmESun = _Km * fESun;

static const float fKr4PI = _Kr * 4.0 * PI;

static const float fKm4PI = _Km * 4.0 * PI;

static const float fScale = 1.0 / (_OuterRadius - _InnerRadius);;

static const float fScaleDepth = 0.25;

static const float fScaleOverScaleDepth = fScale / fScaleDepth;

static const float g = -0.999f;

static const float g2 = g * g;

v2f vert (appdata v)

{

v2f o;

float4 vt = v.vertex;

o.vertex = UnityObjectToClipPos(vt);

o.uv = TRANSFORM_TEX(v.uv, _MainTex);

o.worldPos = mul(unity_ObjectToWorld, vt).xyz;

return o;

}

float Scale(float fcos){

float x = 1.0 - fcos;

return fScaleDepth * exp(-0.00287 + x * (0.459 + x * (3.83 + x * (-6.8 + x * 5.25))));

}

fixed4 frag (v2f i) : SV_Target

{

float3 worldPos = i.worldPos;

float3 v3CameraPos = _WorldSpaceCameraPos;

v3CameraPos.y = fInnerRadius;

float3 v3LightDir = normalize(UnityWorldSpaceLightDir(worldPos));

float3 v3Ray = worldPos - v3CameraPos;

float fFar = length(v3Ray);

v3Ray /= fFar;

float3 v3Start = v3CameraPos;

float fCameraHeight = length(v3CameraPos);

float fStartAngle = dot(v3Ray, v3Start) / fCameraHeight;

float fStartDepth = exp(fScaleOverScaleDepth * (fInnerRadius - fCameraHeight));

float fStartOffset = fStartDepth * Scale(fStartAngle);

float fSampleLength = fFar / fSamples;

float fScaledLength = fSampleLength * fScale;

float3 v3SampleRay = v3Ray * fSampleLength;

float3 v3SamplePoint = v3Start + v3SampleRay * 0.5;

float3 v3FrontColor = 0.0;

for(int n = 0; n < int(fSamples); n++){

float fHeight = length(v3SamplePoint);

float fDepth = exp(fScaleOverScaleDepth * (fInnerRadius - fHeight));

float fLightAngle = dot(v3LightDir, v3SamplePoint) / fHeight;

float fCameraAngle = dot(v3Ray, v3SamplePoint) / fHeight;

float fScatter = (fStartOffset + fDepth * (Scale(fLightAngle) - Scale(fCameraAngle)));

float3 v3Attenuate = exp(-fScatter * (v3InvWaveLength * fKr4PI + fKm4PI));

v3FrontColor += v3Attenuate * (fDepth * fScaledLength);

v3SamplePoint += v3SampleRay;

}

float3 c0 = v3FrontColor * (v3InvWaveLength * fKrESun);

float3 c1 = v3FrontColor * fKmESun;

float3 v3Direction = v3CameraPos - worldPos;

float fcos = dot(v3LightDir, v3Direction) / length(v3Direction);

float fcos2 = fcos * fcos;

float rayleighPhase = 0.75 * (1.0 + fcos2);

float miePhase = 1.5 * ((1.0 - g2) / (2.0 + g2)) * (1.0 + fcos2) / pow(1.0 + g2 - 2.0 * g * fcos, 1.5);

fixed4 col = 1.0;

col.rgb = rayleighPhase * c0 + miePhase * c1;

return col;

}

ENDCG

}

実行結果

　上記シェーダーの実行結果は以下の通りです。InnerRadius=10000、OuterRadius=10250、Kr=0.0025、Km=0.001としています。また、シェーダーを使用するsphereの大きさは20500、カメラ位置は(0, 10000, 0)です。

シェーダーの変更

　このシェーダーでは球の大きさがOuterRadiusと一致していなければなりません。そこで、球の大きさに関わらず実行できるようにシェーダーを変更しました。計算に使用する頂点のワールド座標を半径がOuterRadiusの球の座標となるように変更しています。また、_OuterRadiusと実際の球の大きさ(_SphereRadius)の比をとり、その値をカメラ座標に掛けることで、 OuterRadiusに応じた座標へ変更しています。

_SphereRadius("SphereRadius", Float) = 5125
･･･
static const  float rat = _OuterRadius / _SphereRadius;
･･･
v2f vert (appdata v)
{
	v2f o;
	float4 vt = v.vertex;
	o.vertex = UnityObjectToClipPos(vt);
	o.uv = TRANSFORM_TEX(v.uv, _MainTex);
	o.worldPos = normalize(mul(unity_ObjectToWorld, vt).xyz) * fOuterRadius;
return o;
}
･･･
fixed4 frag (v2f i) : SV_Target
{
	float3 worldPos = i.worldPos;
	float3 v3CameraPos = _WorldSpaceCameraPos * rat;
･･･

_SphereRadius("SphereRadius", Float) = 5125

･･･

static const float rat = _OuterRadius / _SphereRadius;

･･･

v2f vert (appdata v)

{

v2f o;

float4 vt = v.vertex;

o.vertex = UnityObjectToClipPos(vt);

o.uv = TRANSFORM_TEX(v.uv, _MainTex);

o.worldPos = normalize(mul(unity_ObjectToWorld, vt).xyz) * fOuterRadius;

return o;

}

･･･

fixed4 frag (v2f i) : SV_Target

{

float3 worldPos = i.worldPos;

float3 v3CameraPos = _WorldSpaceCameraPos * rat;

･･･

実行結果

　変更したシェーダーの実行結果は以下の通りです。InnerRadius=10000、OuterRadius=10250、 SphereRadius=5125, Kr=0.0025、Km=0.001としています。また、シェーダーを使用するsphereの大きさは10250、カメラ位置は(0, 5000, 0)です。

球の大きさを半分にしましたが、先ほどと同様の結果が得られました。

Skyboxでの使用

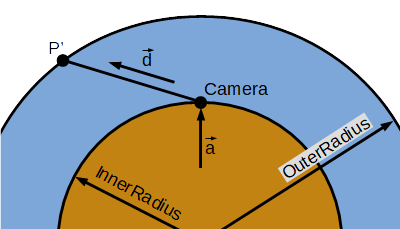
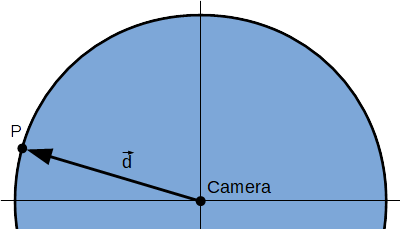
　図1に示すように、今までは大気中にカメラがあることを想定して計算を行っていました。しかし、Skyboxで使用するにあたり、大気中とされる位置までカメラを移動させるのはあまり現実的ではありません。そこで、図2に示すようにカメラの高さが0のとき、図1の場合と同じ結果が得られるようにコードを変更しました。

図1.大気散乱を計算する際のモデル

図2.スカイボックスにおけるベクトルと座標

　図2におけるカメラから任意の点$P$へ向かうベクトル$\vec d$に平行でかつ図1のカメラの位置を通る直線$l$と大気の外側の交点を $P'(x,y,z) $ とします。点$P$と点$P’$においてカメラからの方向は一致します。よって、点 $P$において点$P’$の計算結果が得られるように処理すればよいということになります。よって、点 $P$の座標を点$P’$の座標へ置き換える処理を加えます。

　点 $P’$の座標を計算するための式を求めます。カメラの位置を表すベクトル$\vec{a}$を通り、カメラから大気の外側に向かうベクトル$\vec{d}$に平行な直線のベクトル方程式は

$$ \vec{p’}=\vec{a}+t\vec{d}　\tag{1} $$

となります。ここで、$t$は媒介変数です。この式は以下のように表せます。

$$ \begin{align} \left\{ \begin{array}{l} x&=a_{x}+td_{x}\\ y&=a_{y}+td_{y}\\ z&=a_{z}+td_{z} \end{array} \right.　\tag{2} \end{align} $$

また、球の式は以下の通りです。

$$ x^{2}+y^{2}+z^{2}=r^{2} \tag{3} $$

式$(2)$を式 $(3)$に代入すると、大気の外側と直線$l$の交点における$t$を求めることができます。

$$ (a_{x}+td_{x})^{2}+(a_{x}+td_{x})^{2}+(a_{x}+td_{x})^{2}-r^2=0\\ (d_{x}^{2}+d_{y}^{2}+d_{z}^{2})t^{2}+2(a_{x}d_{x}+a_{y}d_{y}+a_{z}d_{z})t+a_{x}^{2}+a_{y}^{2}+a_{z}^{2}-r^{2}=0 $$

上式は内積を用いることで

$$ \vec{d} \cdot \vec{d}t^{2}+2\vec{a} \cdot \vec{d}t+\vec{a} \cdot \vec{a}-r^{2}=0 \tag{4} $$

となります。ここで、$\vec d$を正規化します。すると、$\vec{d} \cdot \vec{d}$は$1$となります。よって、上式は以下のようになります。

$$ t^{2}+2\vec{a} \cdot \vec{d}t+\vec{a} \cdot \vec{a}-r^{2}=0 \tag{5} $$

解の公式より$t$は

$$ \begin{align} t&=\frac{2\vec a \cdot \vec d\pm \sqrt{(2\vec a \cdot \vec d)^2-4(\vec{a} \cdot \vec{a}-r^{2})}}{2}\\ &=\vec a \cdot \vec d\pm \sqrt{(\vec a \cdot \vec d)^2-\vec{a} \cdot \vec{a}+r^{2}} \end{align} $$

と求まります。球と直線 $l$の交点はカメラが球の内部にある場合は二か所存在します。このシェーダーにおいては$\vec d$方向の座標のみ必要となります。媒介変数$t$が正の時$\vec d$方向の座標が得られるので、求めるべき$t$は以下の式となります。

$$ t=\vec a \cdot \vec d + \sqrt{(\vec a \cdot \vec d)^2-\vec{a} \cdot \vec{a}+r^{2}} \tag{6} $$

式$(6)$より得られる$t$を式$(2)$へ代入することで点$P’$の座標を求めることができます。

shader

　作成したシェーダーは以下の通りです。IntersectionPosで座標を計算しています。また、計算に使用するカメラ位置は固定しています。

Shader "Sky/Skybox_Rayleigh"
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
		_InnerRadius("InnerRadius", Float) = 10000
		_OuterRadius("OuterRadius", Float) = 10250
		_Kr("RayleighScatteringCoefficient", Float) = 0.0025
		_Km("MieScatteringCoefficient", Float) = 0
    }
    SubShader
    {
		Tags { "RenderType"="Background" "Queue"="Background" "Preview Type"="Skybox"}

        Pass
        {
			Tags { "LightMode"="ForwardBase" }

			Cull Off

			CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

			#define PI 3.14159265359

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 vertex : SV_POSITION;
				float3 worldPos :TEXCOORD1;
            };

            sampler2D _MainTex;
            float4 _MainTex_ST;
			
			float _InnerRadius;
			float _OuterRadius;

			float _Kr;
			float _Km;

			static const float fSamples = 2.0;

			static const float3 three_primary_colors = float3(0.68, 0.55, 0.44);
			static const float3 v3InvWaveLength = 1.0 / pow(three_primary_colors, 4.0);

			static const float fOuterRadius = _OuterRadius;
			static const float fInnerRadius = _InnerRadius;

			static const float fESun = 20.0;
			static const float fKrESun = _Kr * fESun;
			static const float fKmESun = _Km * fESun;

			static const float fKr4PI = _Kr * 4.0 * PI;
			static const float fKm4PI = _Km * 4.0 * PI;

			static const float fScale = 1.0 / (_OuterRadius - _InnerRadius);;
			static const float fScaleDepth = 0.25;
			static const float fScaleOverScaleDepth = fScale / fScaleDepth;

			static const float g = -0.999f;
			static const float g2 = g * g;

            v2f vert (appdata v)
            {
                v2f o;
				float4 vt = v.vertex;
                o.vertex = UnityObjectToClipPos(vt);
                o.uv = TRANSFORM_TEX(v.uv, _MainTex);
				o.worldPos = normalize(mul(unity_ObjectToWorld, vt).xyz) * fOuterRadius;
                return o;
            }

			float Scale(float fcos){
				float x = 1.0 - fcos;
				return fScaleDepth * exp(-0.00287 + x * (0.459 + x * (3.83 + x * (-6.8 + x * 5.25))));
			}

			float3 IntersectionPos(float3 dir, float3 a, float radius)
			{
				float b = dot(a, dir);
				float c = dot(a, a) - radius * radius;
				float d = max(b * b - c, 0.0);

				return a + dir * (-b + sqrt(d));
			}

            fixed4 frag (v2f i) : SV_Target
            {
				float3 worldPos = i.worldPos;
				worldPos = IntersectionPos(normalize(worldPos), float3(0.0, fInnerRadius, 0.0), fOuterRadius);
				float3 v3CameraPos =  float3(0.0, fInnerRadius, 0.0);
				float3 v3LightDir = normalize(UnityWorldSpaceLightDir(worldPos));

				float3 v3Ray = worldPos - v3CameraPos;
				float fFar = length(v3Ray);
				v3Ray /= fFar;

				float3 v3Start = v3CameraPos;
				float fCameraHeight = length(v3CameraPos);
				float fStartAngle = dot(v3Ray, v3Start) / fCameraHeight;
				float fStartDepth = exp(fScaleOverScaleDepth * (fInnerRadius - fCameraHeight));
				float fStartOffset = fStartDepth * Scale(fStartAngle);

				float fSampleLength = fFar / fSamples;
				float fScaledLength = fSampleLength * fScale;
				float3 v3SampleRay = v3Ray * fSampleLength;
				float3 v3SamplePoint = v3Start + v3SampleRay * 0.5;

				float3 v3FrontColor = 0.0;
				for(int n = 0; n < int(fSamples); n++){
					float fHeight = length(v3SamplePoint);
					float fDepth = exp(fScaleOverScaleDepth * (fInnerRadius - fHeight));
					float fLightAngle = dot(v3LightDir, v3SamplePoint) / fHeight;
					float fCameraAngle = dot(v3Ray, v3SamplePoint) / fHeight;
					float fScatter = (fStartOffset + fDepth * (Scale(fLightAngle) - Scale(fCameraAngle)));
					float3 v3Attenuate = exp(-fScatter * (v3InvWaveLength * fKr4PI + fKm4PI));
					v3FrontColor += v3Attenuate * (fDepth * fScaledLength);
					v3SamplePoint += v3SampleRay;
				}

				float3 c0 = v3FrontColor * (v3InvWaveLength * fKrESun);
				float3 c1 = v3FrontColor * fKmESun;
				float3 v3Direction = v3CameraPos - worldPos;

				float fcos = dot(v3LightDir, v3Direction) / length(v3Direction);
				float fcos2 = fcos * fcos;

				float rayleighPhase = 0.75 * (1.0 + fcos2);
				float miePhase = 1.5 * ((1.0 - g2) / (2.0 + g2)) * (1.0 + fcos2) / pow(1.0 + g2 - 2.0 * g * fcos, 1.5);

				fixed4 col = 1.0;
				col.rgb = rayleighPhase * c0 + miePhase * c1;
                return col;
            }
            ENDCG
        }
    }
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

Shader "Sky/Skybox_Rayleigh"

{

Properties

{

_MainTex ("Texture", 2D) = "white" {}

_InnerRadius("InnerRadius", Float) = 10000

_OuterRadius("OuterRadius", Float) = 10250

_Kr("RayleighScatteringCoefficient", Float) = 0.0025

_Km("MieScatteringCoefficient", Float) = 0

}

SubShader

{

Tags { "RenderType"="Background" "Queue"="Background" "Preview Type"="Skybox"}

Pass

{

Tags { "LightMode"="ForwardBase" }

Cull Off

CGPROGRAM

#pragma vertex vert

#pragma fragment frag

#include "UnityCG.cginc"

#define PI 3.14159265359

struct appdata

{

float4 vertex : POSITION;

float2 uv : TEXCOORD0;

};

struct v2f

{

float2 uv : TEXCOORD0;

float4 vertex : SV_POSITION;

float3 worldPos :TEXCOORD1;

};

sampler2D _MainTex;

float4 _MainTex_ST;

float _InnerRadius;

float _OuterRadius;

float _Kr;

float _Km;

static const float fSamples = 2.0;

static const float3 three_primary_colors = float3(0.68, 0.55, 0.44);

static const float3 v3InvWaveLength = 1.0 / pow(three_primary_colors, 4.0);

static const float fOuterRadius = _OuterRadius;

static const float fInnerRadius = _InnerRadius;

static const float fESun = 20.0;

static const float fKrESun = _Kr * fESun;

static const float fKmESun = _Km * fESun;

static const float fKr4PI = _Kr * 4.0 * PI;

static const float fKm4PI = _Km * 4.0 * PI;

static const float fScale = 1.0 / (_OuterRadius - _InnerRadius);;

static const float fScaleDepth = 0.25;

static const float fScaleOverScaleDepth = fScale / fScaleDepth;

static const float g = -0.999f;

static const float g2 = g * g;

v2f vert (appdata v)

{

v2f o;

float4 vt = v.vertex;

o.vertex = UnityObjectToClipPos(vt);

o.uv = TRANSFORM_TEX(v.uv, _MainTex);

o.worldPos = normalize(mul(unity_ObjectToWorld, vt).xyz) * fOuterRadius;

return o;

}

float Scale(float fcos){

float x = 1.0 - fcos;

return fScaleDepth * exp(-0.00287 + x * (0.459 + x * (3.83 + x * (-6.8 + x * 5.25))));

}

float3 IntersectionPos(float3 dir, float3 a, float radius)

{

float b = dot(a, dir);

float c = dot(a, a) - radius * radius;

float d = max(b * b - c, 0.0);

return a + dir * (-b + sqrt(d));

}

fixed4 frag (v2f i) : SV_Target

{

float3 worldPos = i.worldPos;

worldPos = IntersectionPos(normalize(worldPos), float3(0.0, fInnerRadius, 0.0), fOuterRadius);

float3 v3CameraPos = float3(0.0, fInnerRadius, 0.0);

float3 v3LightDir = normalize(UnityWorldSpaceLightDir(worldPos));

float3 v3Ray = worldPos - v3CameraPos;

float fFar = length(v3Ray);

v3Ray /= fFar;

float3 v3Start = v3CameraPos;

float fCameraHeight = length(v3CameraPos);

float fStartAngle = dot(v3Ray, v3Start) / fCameraHeight;

float fStartDepth = exp(fScaleOverScaleDepth * (fInnerRadius - fCameraHeight));

float fStartOffset = fStartDepth * Scale(fStartAngle);

float fSampleLength = fFar / fSamples;

float fScaledLength = fSampleLength * fScale;

float3 v3SampleRay = v3Ray * fSampleLength;

float3 v3SamplePoint = v3Start + v3SampleRay * 0.5;

float3 v3FrontColor = 0.0;

for(int n = 0; n < int(fSamples); n++){

float fHeight = length(v3SamplePoint);

float fDepth = exp(fScaleOverScaleDepth * (fInnerRadius - fHeight));

float fLightAngle = dot(v3LightDir, v3SamplePoint) / fHeight;

float fCameraAngle = dot(v3Ray, v3SamplePoint) / fHeight;

float fScatter = (fStartOffset + fDepth * (Scale(fLightAngle) - Scale(fCameraAngle)));

float3 v3Attenuate = exp(-fScatter * (v3InvWaveLength * fKr4PI + fKm4PI));

v3FrontColor += v3Attenuate * (fDepth * fScaledLength);

v3SamplePoint += v3SampleRay;

}

float3 c0 = v3FrontColor * (v3InvWaveLength * fKrESun);

float3 c1 = v3FrontColor * fKmESun;

float3 v3Direction = v3CameraPos - worldPos;

float fcos = dot(v3LightDir, v3Direction) / length(v3Direction);

float fcos2 = fcos * fcos;

float rayleighPhase = 0.75 * (1.0 + fcos2);

float miePhase = 1.5 * ((1.0 - g2) / (2.0 + g2)) * (1.0 + fcos2) / pow(1.0 + g2 - 2.0 * g * fcos, 1.5);

fixed4 col = 1.0;

col.rgb = rayleighPhase * c0 + miePhase * c1;

return col;

}

ENDCG

}

実行結果

上記シェーダーの実行結果は以下の通りです。Skyboxでも問題なく空の色が描画されていることがわかります。

参考サイト

GPU Gems 2：Chapter 16. Accurate Atmospheric Scattering

agehama’s diary：ピクセルシェーダで空を描く

FTEXT：直線のベクトル方程式

前の記事

法線ベクトルの再計算 2019.07.02
次の記事

平面の鏡面反射(Cubemap) 2019.10.14

空の色（大気散乱シミュレーション）

シェーダーの作成

shader

実行結果

シェーダーの変更

実行結果

Skyboxでの使用

shader

実行結果

参考サイト

法線ベクトルの再計算 2019.07.02

平面の鏡面反射(Cubemap) 2019.10.14