法線ベクトルの再計算

2019.07.02
Unity
shader

　シェーダで頂点を移動すると、元の法線ベクトルは使用できなくなります。そのため、法線ベクトルを再計算する必要があります。法線ベクトルは隣接する頂点もしくはハイトマップから計算することができます。

1. 隣接する頂点を利用する方法
- 1.1. shader
- 1.2. 実行結果
2. ハイトマップから法線を計算する方法
- 2.1. shader
- 2.2. 実行結果
3. 参考ページ

隣接する頂点を利用する方法

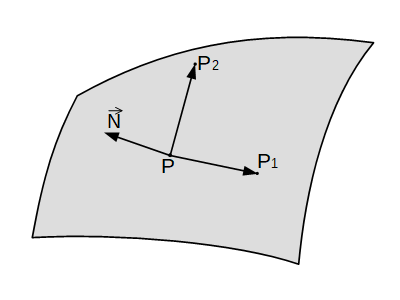
　法線ベクトルは、ある点とその近傍の二点の座標を用いることで求めることができます。ある点 $P$ における法線ベクトルを求めるには、点 $P$ から接ベクトル方向へ少し移動した点$P_{1}$と従法線ベクトル方向へ少し移動した点$P_{2}$を求めます。これらの点から二つのベクトル$P_{1}-P$と $P_{2}-P$ を求め、このベクトルの外積$(P_{2}-P)\times (P_{1}-P )$を計算すると法線ベクトルが求まります。

座標系は左手系であるため、外積によって求められる法線ベクトル $\vec{N}$ は上図の方向となっています(左手系において、外積によって得られるベクトルの方向は右手系の逆となる)。

shader

　パーリンノイズによって変形させたオブジェクトの法線ベクトルを再計算し、ランバート反射によるライティングを行っています。

Shader "Unlit/ReCuluNormal"
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
		_Color ("Color", Color) = (1.0, 1.0, 1.0, 1.0)
		_NoiseScale ("NoiseScale", Range(0.1, 5.0)) = 1
		_NoiseStrength ("NoiseStrength", Range(0.1, 1.0)) = 1
		_Seed ("Seed", Int) = 1
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }

        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
				float3 normal : NORMAL;
				float4 tangent : TANGENT;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 vertex : SV_POSITION;
				float3 normal : NORMAL;
				float4 tangent : TANGENT;
				float4 pos : TEXCOORD2;
            };

            sampler2D _MainTex;
            float4 _MainTex_ST;

			float4 _Color;
			float _NoiseScale;
			float _NoiseStrength;
			int _Seed;

 			float3 rand3d(float3 p, int seed)
			{
				float3 s = float3(dot(p, float3(127.1, 311.7, 74.7)) + seed,
								  dot(p, float3(269.5, 183.3, 246.1)) + seed,
								  dot(p, float3(113.5, 271.9, 124.6)) + seed);
				return -1.0 + 2.0 * frac(sin(s) * 43758.5453123);
			}

			float noise3(float3 st, int seed)
			{
				float3 p = floor(st);
				float3 f = frac(st);

				float w000 = dot(rand3d(p, seed), f);
				float w100 = dot(rand3d(p + float3(1, 0, 0), seed), f - float3(1, 0, 0));
				float w010 = dot(rand3d(p + float3(0, 1, 0), seed), f - float3(0, 1, 0));
				float w110 = dot(rand3d(p + float3(1, 1, 0), seed), f - float3(1, 1, 0));
				float w001 = dot(rand3d(p + float3(0, 0, 1), seed), f - float3(0, 0, 1));
				float w101 = dot(rand3d(p + float3(1, 0, 1), seed), f - float3(1, 0, 1));
				float w011 = dot(rand3d(p + float3(0, 1, 1), seed), f - float3(0, 1, 1));
				float w111 = dot(rand3d(p + float3(1, 1, 1), seed), f - float3(1, 1, 1));
				
				float3 u = f * f * (3.0 - 2.0 * f);

				float r1 = lerp(lerp(w000, w100, u.x), lerp(w010, w110, u.x), u.y);
				float r2 = lerp(lerp(w001, w101, u.x), lerp(w011, w111, u.x), u.y);

				return lerp(r1, r2, u.z);
			}

            v2f vert (appdata v)
            {
                v2f o;
				float noiseScale = _NoiseScale;
				float noiseStr = _NoiseStrength;
				float4 vt = v.vertex;
				o.pos = vt;

				float delta = 0.05;
				float3 normal = v.normal;
				float4 tangent = v.tangent;
				float3 binormal = normalize(cross(normal, tangent.xyz)) * tangent.w;

				vt.xyz += normal * noise3(vt * noiseScale, _Seed) * noiseStr;

                o.vertex = UnityObjectToClipPos(vt);
                o.uv = TRANSFORM_TEX(v.uv, _MainTex);
				o.normal = normal;
				o.tangent = tangent;
                return o;
            }

            fixed4 frag (v2f i) : SV_Target
            {
				float noiseScale = _NoiseScale;
				float noiseStr = _NoiseStrength;
				int seed = _Seed;

				float delta = 0.05;
				float3 normal = i.normal;
				float4 tangent = i.tangent;
				float3 binormal = normalize(cross(normal, tangent.xyz)) * tangent.w;

				float4 vt = i.pos;

				vt.xyz += normal * noise3(vt * noiseScale, seed) * noiseStr;

				float3 vt1 = vt + tangent.xyz * delta;
				vt1.xyz += normal * noise3(vt1 * noiseScale, seed) * noiseStr;

				float3 vt2 = vt + binormal * delta;;
				vt2.xyz += normal * noise3(vt2 * noiseScale, seed) * noiseStr;

				normal = normalize(cross(vt2 - vt, vt1 - vt));

				float3 lightDir = normalize(ObjSpaceLightDir(vt));
				float4 diff = saturate(dot(normal, lightDir));
				
                fixed4 col = 1.0;
				col.rgb = _Color * diff;
                return col;
            }
            ENDCG
        }
    }
}

tangent.wにDirectX(左手系)の場合は1、OpenGL(右手系)の場合は-1が入っています。このtangent.wを従法線方向のベクトルに掛けることで、座標系が異なった場合でも外積によって得られる法線ベクトルが一致するように処理できます。

実行結果

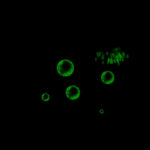
　上記シェーダの実行結果は以下の通りです。ノイズによって変形した球体にその形状に伴った陰影が得られていることがわかります。

また、法線ベクトルを表示すると以下のようになります。

ハイトマップから法線を計算する方法

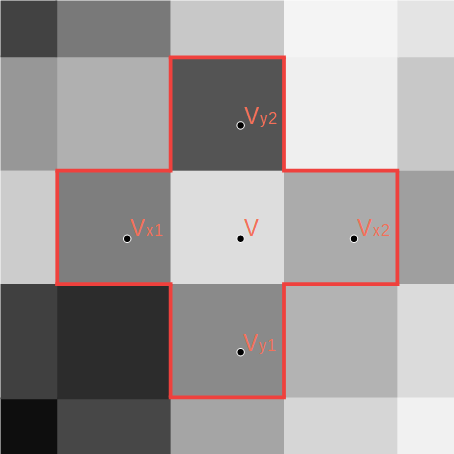
　Unityにおいては、ハイトマップはTextureTypeをNormal Mapへ変更し、Create from Grayscaleにチェックを入れることでノーマプマップへ変換することができます。しかしながら、波紋のようにリアルタイムで変化する場合はシェーダでハイトマップから法線ベクトルを計算する必要があります。この法線ベクトルは下図に示すように、あるテクセルに隣接するテクセルの情報を利用することで計算できます。

　$V_{x1}$ 、$V$及び$V_{x2}$の三点を結ぶ二次曲線を求め、Vにおける二次曲線の傾き$du$を求めるます。同様に、 $V_{y1}$ 、$V$及び$V_{y2}$の三点を結ぶ二次曲線を求め、Vにおける二次曲線の傾き $dv$を求めます。

$$ du = \frac{v_{x2}-v_{x1}}{2},\ dv = \frac{v_{y2}-v_{y1}}{2} $$

これらの傾きから$x$方向及び $y$方向の接ベクトルがわかります。 Unityではy軸が上方向ですが、法線マップではz軸が上となります。そのため、それぞれのベクトルは以下のようになります。

$$ \vec{T_{x}}=(1,\ 0,\ du),\ \vec{T_{y}}=(0,\ 1,\ dv)\\ $$

これらの接ベクトルの外積を求めることで法線ベクトル$N$が求まります。

$$ \begin{align} \vec{N}&=\vec{T_{x}}\times \vec{T_{y}}\\ &=(-du,\ -dv,\ 1)\\ \end{align} $$

詳しい導出過程は○×（まるぺけ）つくろーどっとコム:その３波：ハイトマップから法線マップを作る方法に記載されています。

shader

　波動方程式を用いた波紋の作成によって得られるハイトマップ(_HightMap)から法線ベクトルを計算し、平面の鏡面反射(_ReflectionTex)によって得られるテクスチャを法線ベクトルによって歪めることで、鏡面反射となっている平面が波紋によって波打つ様子を描画しています。また、BumpScaleによって歪む量を調節することができます。

Shader "Unlit/WaveReflection"
{
	Properties
	{
		_MainTex ("Texture", 2D) = "white" {}
		_ReflectionTex ("ReflectionTexture", 2D) = "white" {}
		_HeightMap ("HeightMap", 2D) = "black" {}
		_BumpScale ("BunpScale", Range(0.0, 20.0)) = 1
	}
	SubShader
	{
        Tags { "RenderType"="Opaque" }

		Pass
		{
			CGPROGRAM
			#pragma vertex vert
			#pragma fragment frag
			
			#include "UnityCG.cginc"

			struct appdata
			{
				float4 vertex : POSITION;
				float2 uv : TEXCOORD0;
				float3 normal : NORMAL;
			};

			struct v2f
			{
				float2 uv : TEXCOORD0;
				float4 vertex : SV_POSITION;
				float4 projCoord : TEXCOORD1;
			};

			sampler2D _MainTex;
			float4 _MainTex_ST;
			sampler2D _ReflectionTex;
			float4 _ReflectionTex_ST;
			sampler2D _HeightMap;
			float4 _HeightMap_ST;
			float4 _HeightMap_TexelSize;

			float _BumpScale;
			
			v2f vert (appdata v)
			{
				v2f o;
				o.vertex = UnityObjectToClipPos(v.vertex);
				o.uv = TRANSFORM_TEX(v.uv, _MainTex);
				o.projCoord = ComputeScreenPos(o.vertex);
				return o;
			}
			
			fixed4 frag (v2f i) : SV_Target
			{
				float3 duv = float3(_HeightMap_TexelSize.x, _HeightMap_TexelSize.y, 0.0);
				float du = tex2D(_HeightMap, i.uv + duv.xz).r - tex2D(_HeightMap, i.uv - duv.xz).r;
				float dv = tex2D(_HeightMap, i.uv + duv.zy).r - tex2D(_HeightMap, i.uv - duv.zy).r;
				//float3 normal = normalize(cross(float3(1.0, 0.0, du), float3(0.0, 1.0, dv)));
				float3 normal = normalize(float3(-du, -dv, 1.0));

				normal = normalize(float3(normal.xy * _BumpScale, normal.z));
				i.projCoord.xyz += normal.xyz;
				fixed4 col = tex2Dproj(_ReflectionTex, UNITY_PROJ_COORD(i.projCoord));
				col.a = 1;

				return col;
			}
			ENDCG
		}
	}
}