シェーダでトランジション(図形)

外周から回るトランジション
長方形を利用して外側から内側へ回りながら画面を黒くするシェーダを作成しました。
shader
作成したシェーダは以下の通りです。
Shader "Transition/Transition_Rotation"
{
Properties
{
_MainTex ("Texture", 2D) = "white" {}
_Div ("Division Size", Int) = 10
_Size ("Size", Range(0.01, 2)) = 1
_Value ("Value", Range(0, 100)) = 0
_Rotation ("Rotation", Range(0, 360)) = 0
[MaterialToggle] _Direction ("Rotation Direction", Float) = 0
[MaterialToggle] _Aspect ("Aspect Ratio", Float) = 0
}
SubShader
{
Tags { "RenderType"="Transparent" "RenderType"="Transparent" }
Blend SrcAlpha OneMinusSrcAlpha
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float2 uv : TEXCOORD0;
float4 vertex : SV_POSITION;
};
sampler2D _MainTex;
float4 _MainTex_ST;
int _Div;
float _Size;
float _Value;
float _Rotation;
int _Direction;
int _Aspect;
v2f vert (appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = TRANSFORM_TEX(v.uv, _MainTex);
return o;
}
//rectangle
float rectangle(float2 p, float2 size){
return max(abs(p.x) - size.x, abs(p.y) - size.y);
}
float2 rotation(float2 p, float theta){
return float2((p.x) * cos(theta) - p.y * sin(theta), p.x * sin(theta) + p.y * cos(theta));
}
float trs(float2 p, float val, float div, float t)
{
float mn = 0.0001;
float u = 1.0;
for(int i = 0; i < t; i++){
u += (div * 2.0 - 4.0 * i - 2.0) * 4.0;
}
float r = (div * 2.0 - 4.0 * t - 2.0);
float sc = val - u;
float a = 1;
float rect = rectangle(p - float2(-div + t * 2.0, -div + t * 2.0 + 1.0), float2(sc, mn));
a = 1 - step(1.0, rect);
rect = rectangle(p - float2(div - t * 2.0 - 1.0, -div + (t + 1.0) * 2.0), float2(mn, sc - r - 2.0));
a = max(a, 1 - step(1.0, rect));
rect = rectangle(p - float2(div - (t + 1) * 2.0, div - t * 2.0 - 1.0), float2(sc - r * 2.0 - 2.0, mn));
a = max(a, 1 - step(1.0, rect));
rect = rectangle(p - float2(-div + t * 2.0 + 1.0, div - (t + 1) * 2.0), float2(mn, sc - r * 3.0 - 2.0));
a = max(a, 1 - step(1.0, rect));
return a;
}
fixed4 frag (v2f i) : SV_Target
{
float div = _Div;
int dir = _Direction;
int asp = _Aspect;
float ratio = _ScreenParams.x / _ScreenParams.y;
float val = _Value * div * div * 2.0;
float2 f_st = i.uv * 2.0 - 1.0;
//アスペクト比で調整
f_st.x *= (ratio * asp + (1.0 - asp));
//座標の回転
f_st = rotation(f_st, radians(_Rotation));
//回転方向
f_st.x = f_st.x * (1.0 - 2.0 * dir);
f_st *= div;
f_st *= _Size;
float a = 0.0;
for(int i = 0; i < div * 0.5; i++){
a = min(a + trs(f_st, val, div, i), 1);
}
fixed4 col = 0.0;
col.a = a;
return col;
}
ENDCG
}
}
}uv座標(0~1)を(-1~1)へ変更し、これに分割数(div)を掛けることにより-分割数~分割数とします。
float div = _Div;
float2 f_st = i.uv * 2.0 - 1.0;
f_st *= div;高さと幅が2となる長方形を作成します。画像に示すように正方形にはならず、アスペクト比に応じた長方形が表示されます。
float rect = rectangle(f_st, float2(0.0, 0.0));
a = 1 - step(1.0, rect);下画像のように、長方形の下部が画面下、長方形の横半分が表示される座標へ移動させます。
float rect = rectangle(f_st - float2(-div, -div + 1.0), float2(0.0, 0.0));
a = 1 - step(1.0, rect);長方形の大きさをfloat2(-1.0, 0.0)とし、幅を0とします。画像に示すように長方形はなくなります。
float rect = rectangle(f_st - float2(-div, -div + 1.0), float2(-1.0, 0.0));
a = 1 - step(1.0, rect);この長方形の横幅をインスペクタから変更できるようにします。
Properties
{
_MainTex ("Texture", 2D) = "white" {}
_Div ("Division Size", Int) = 10
_Value ("Value", Range(0, 100)) = 0
}
・・・
float val = _Value;
float rect = rectangle(f_st - float2(-div, -div + 1.0), float2(val - 1.0, 0.0));
a = 1 - step(1.0, rect);valを0から徐々に大きくすると
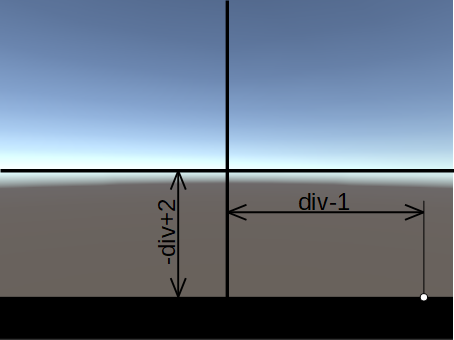
このように、長方形により下側を黒くすることができます。次に右側を作成します。長方形の中心位置を下画像の場所とします。
rect = rectangle(f_st - float2(div - 1.0, -div + 2.0), float2(0.0, val - 1.0));
a = max(a, 1 - step(1.0, rect));このままでは、下側の長方形と右側の長方形が同時に変化してしまいます。下側の長方形が画面端まで大きくなった後に、右側の長方形を大きくし始めたいので、下側の長方形が画面端に到達する大きさ(div*2)を右側の長方形の大きさから引きます。
rect = rectangle(f_st - float2(div - 1.0, -div + 2.0), float2(0.0, val - div * 2.0 - 1.0));
a = max(a, 1 - step(1.0, rect));さらに、上側と左側の長方形を作成します。
float rect = rectangle(f_st - float2(-div, -div + 1.0), float2(val - 1.0, 0.0));
a = 1 - step(1.0, rect);
rect = rectangle(f_st - float2(div - 1.0, -div + 2.0), float2(0.0, val - div * 2.0 - 1.0));
a = max(a, 1 - step(1.0, rect));
rect = rectangle(f_st - float2(div - 2.0, div - 1.0), float2(val - div * 4.0 + 1.0, 0.0));
a = max(a, 1 - step(1.0, rect));
rect = rectangle(f_st - float2(-div + 1.0, div - 2.0), float2(0.0, val - div * 6.0 + 3.0));
a = max(a, 1 - step(1.0, rect));これを実行すると
このように外周を回りながら黒くすることができました。
次に二周目の長方形を作成します。一週目の全ての長方形の長さは(div * 2.0 - 2.0) * 4.0となります。そのため、長方形の大きさから(div * 2.0 - 2.0) * 4.0を減算しています。
rect = rectangle(f_st - float2(-div + 2.0, -div + 3.0),
float2(val - (div * 2.0 - 2.0) * 4.0 - 1.0, 0.0));
a = max(a, 1 - step(1.0, rect));
rect = rectangle(f_st - float2(div - 3.0, -div + 4.0),
float2(0.0, val - (div * 2.0 - 2.0) * 4.0 - 1.0 - div * 2.0 + 4.0));
a = max(a, 1 - step(1.0, rect));
rect = rectangle(f_st - float2(div - 4.0, div - 3.0),
float2(val - (div * 2.0 - 2.0) * 4.0 - 1.0 - div * 4.0 + 10.0, 0.0));
a = max(a, 1 - step(1.0, rect));
rect = rectangle(f_st - float2(-div + 3.0, div - 4.0),
float2(0.0, val - (div * 2.0 - 2.0) * 4.0 - 1.0 - div * 6.0 + 16.0));
a = max(a, 1 - step(1.0, rect));以上より任意の周回(t)におけるコードは以下のようになります。場合によっては長方形の隙間が生じます。これを回避するため、mnによって長方形の幅を少し大きくしています。
float trs(float2 p, float val, float div, float t)
{
float mn = 0.001;
float u = 1.0;
for(int i = 0; i < t; i++){
u += (div * 2.0 - 4.0 * i - 2.0) * 4.0;
}
float r = (div * 2.0 - 4.0 * t - 2.0);
float sc = val - u;
float a = 1;
float rect = rectangle(p - float2(-div + t * 2.0, -div + t * 2.0 + 1.0), float2(sc, mn));
a = 1 - step(1.0, rect);
rect = rectangle(p - float2(div - t * 2.0 - 1.0, -div + (t + 1.0) * 2.0), float2(mn, sc - r - 2.0));
a = max(a, 1 - step(1.0, rect));
rect = rectangle(p - float2(div - (t + 1) * 2.0, div - t * 2.0 - 1.0), float2(sc - r * 2.0 - 2.0, mn));
a = max(a, 1 - step(1.0, rect));
rect = rectangle(p - float2(-div + t * 2.0 + 1.0, div - (t + 1) * 2.0), float2(mn, sc - r * 3.0 - 2.0));
a = max(a, 1 - step(1.0, rect));
return a;
}この関数をfor文によって0~分割数の半分まで実行することで、長方形が周回しながら画面を覆うようになります。
for(int i = 0; i < div * 0.5; i++){
a = min(a + trs(f_st, val, div, i), 1);
}次に回転方向を変更できるようにします。x座標を反転させれば回転方向を逆にできます。よって
Properties
{
・・・
[MaterialToggle] _Direction ("Rotation Direction", Float) = 0
}
・・・
f_st.x = f_st.x * (1.0 - 2.0 * dir);とすると、インスペクタのRotetion Directionへチェックを入れることで回転方向を変更できます。さらに、開始位置を座標を回転することで変更できるようにしました。
Properties
{
・・・
_Rotation ("Rotation", Range(0, 360)) = 0
}
・・・
float2 rotation(float2 p, float theta){
return float2((p.x) * cos(theta) - p.y * sin(theta), p.x * sin(theta) + p.y * cos(theta));
}
・・・
f_st = rotation(f_st, radians(_Rotation));そして、アスペクト比で調整することで長方形から正方形へと変更します。これにより、Rotationが0、90、180及び270以外の値でもきれいに表示されるようになります。ただ、下画像のように、黒く塗りつぶす領域が画面より小さくなってしまいます。
Properties
{
・・・
[MaterialToggle] _Aspect ("Aspect Ratio", Float) = 0
}
・・・
int asp = _Aspect;
float ratio = _ScreenParams.x / _ScreenParams.y;
f_st.x *= (ratio * asp + (1.0 - asp));そのため、座標を縮小することでこれに対応できるようにしています。
Properties
{
・・・
_Size ("Size", Range(0.01, 2)) = 1
・・・
}
・・・
f_st *= _Size;最後に、_Valueの値の範囲が0~1となるように
float val = _Value * div * div * 2.0;としています。高さ2の長方形で2*div+2*divの面積を埋めるため、このような式となっています。
実行結果
以上のシェーダをUIのPanel上で実行すると以下の結果が得られます。外側から内側へぐるぐると回りながら黒く塗りつぶしています。
Division Size=16、Rotation=45、Size=0.6、Aspect Ratioにチェックを入れると以下のような結果が得られます。
複数の図形を使用
前回の記事で同じ種類の図形を複数表示する方法を紹介しました。これを利用して、トランジション用のシェーダを作成しました。
画面端から円が拡がるトランジション
ある方向から直線的に円の大きさが変化するトランジションシェーダを作成しました。
shader
作成したシェーダは以下の通りです。
Shader "Transition/Transition_Cirlce_Slide"
{
Properties
{
_MainTex ("Texture", 2D) = "white" {}
[MaterialToggle] _Inverse ("Inverse", Float) = 0
_Div ("Division Size", Int) = 16
_Value ("Value", Range(0, 1)) = 0
_Width ("Width", Range(0, 1)) = 0
_Dir ("Direction(X, Y)", Vector) = (1, 1, 0, 0)
}
SubShader
{
Tags { "RenderType"="Transparent" "RenderType"="Transparent" }
Blend SrcAlpha OneMinusSrcAlpha
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float2 uv : TEXCOORD0;
float4 vertex : SV_POSITION;
};
sampler2D _MainTex;
float4 _MainTex_ST;
float2 _Dir;
float _Inverse;
float _Div;
float _Width;
float _Value;
v2f vert (appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = TRANSFORM_TEX(v.uv, _MainTex);
return o;
}
//circle
float circle(float2 p){
return dot(p, p);
}
fixed4 frag (v2f i) : SV_Target
{
float inv = _Inverse;
float w = _Width;
float2 div = float2(_Div, _Div * _ScreenParams.y / _ScreenParams.x);
float2 dir = normalize(_Dir);
float val = _Value * (dot(div - 1.0, abs(dir)) * w + 2.0);
float2 st = i.uv * div;
float2 i_st = floor(st);
float2 f_st = frac(st) * 2.0 - 1.0;
float a = 1;
float2 sg = sign(dir);
for(int i = -1; i <= 1; i++){
for(int j = -1; j <= 1; j++){
float2 f = (div - 1.0) * (0.5 - sg * 0.5) + (i_st + float2(i, j)) * sg;
float v = val - dot(f, abs(dir)) * w;
float ci = circle(f_st - float2(2.0 * i, 2.0 * j));
a = min(a, step(v, ci));
//a = min(a, smoothstep(v - 0.1, v, ci));
}
}
fixed4 col = 0.0;
col.a = inv - a * (inv * 2.0 - 1.0);
return col;
}
ENDCG
}
}
}最初に、円を中心に表示させます。図形の描画についてはここに記述しています。lengthを用いて円を描画していましたが、今回は内積によって円の描画をしています。
float circle(float2 p){
return dot(p, p);
}
fixed4 frag (v2f i) : SV_Target
{
float2 f_st = frac(i.uv) * 2.0 - 1.0;
float ci = circle(f_st);
fixed4 col = 0.0;
col.a = step(0.1, ci);
return col;
}表示する円の数(_Div)を決定します。縦方向の円の数はアスペクト比に応じて変化するようにしています。これにより、円がアスペクト比に応じて変形することを防いでいます。この円の数をuv座標に掛けると円を複数表示できます。
Properties
{
_MainTex ("Texture", 2D) = "white" {}
_Div ("Division Size", Int) = 16
}
・・・
fixed4 frag (v2f i) : SV_Target
{
float2 div = float2(_Div, _Div * _ScreenParams.y / _ScreenParams.x);
float2 st = i.uv * div;
float2 f_st = frac(st) * 2.0 - 1.0;
float ci = circle(f_st);
fixed4 col = 0.0;
col.a = step(0.1, ci);
return col;
}円を任意の大きさへ変更できるようにします。
Properties
{
_Value ("Value", Range(-0.5, 16)) = 0
・・・
}
・・・
fixed4 frag (v2f i) : SV_Target
{
float val = _Value;
・・・
col.a = step(v, ci);
return col;
}円が大きくなるタイミングを座標を用いてずらします。座標stの整数部分を求めると図形ごとに座標に応じた整数値 (i_st) が得られます。これを利用して円が大きくなるタイミングをずらします。また、この値に定数(_Width)を掛けることでタイミングを調整することができます。Value=3、Width=0.3のとき下画像のような結果が得られます。
Properties
{
_Width ("Width", Range(0, 1)) = 0
・・・
}
・・・
fixed4 frag (v2f i) : SV_Target
{
・・・
float2 i_st = floor(st);
float v = val - i_st.x * w;
・・・
col.a = step(v, ci);
return col;
}上記のコードでは左から右に円が大きくなっていきます。次は円が大きくなっていく方向を変更できるようにコードを変えます。円が大きくなる方向はベクトル(_Dir)を用いて決定します。まずは、このベクトルを正規化します。signによってベクトルの符号を取り出し、これを利用することによりベクトルの要素がマイナスの時、i_stを逆順(f)にしています。この値(f)と方向を表すベクトルの絶対値の内積によって求まる値で、円ごとに大きくなるタイミングを調整しています。
Properties
{
_Dir ("Direction(X, Y)", Vector) = (1, 1, 0, 0)
・・・
}
float2 _Dir;
・・・
fixed4 frag (v2f i) : SV_Target
{
・・・
float2 dir = normalize(_Dir);
float2 sg = sign(dir);
float2 f = (div - 1) * (0.5 - sg * 0.5) + i_st * sg;
float v = val - dot(f, abs(dir)) * w;
・・・問題が一つあります。円は区切られた領域より大きくなることができません。そのため、円が領域からはみ出した部分は描画されません。
この問題を解決するために、自身の領域の円だけではなく自身と周りの9か所の領域における円を計算し、その円を全て描画するようにしました。これにより、自身の領域にはみ出してきた円を描画できるようになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
float a = 1; float2 sg = sign(dir); for(int i = -1; i <= 1; i++){ for(int j = -1; j <= 1; j++){ float2 f = (div - 1) * (0.5 - sg * 0.5) + (i_st + float2(i, j)) * sg; float v = val - dot(f, abs(dir)) * w; float ci = circle(f_st - float2(2.0 * i, 2.0 * j)); a = min(a, step(v, ci)); } } |
さらに、 最後の円が大きくなり始めるタイミングに円が分割した領域より大きくなる値(2.0)を加算し、valに掛けることで_Valが0~1の範囲となるようにしています。
fixed4 frag (v2f i) : SV_Target
{
・・・
float val = _Value * (dot(div - 1.0, abs(dir)) * w + 2.0);
・・・最後に、円を透明でなく黒く、つまり、反転させて表示できるようにコードを変更しました。
Properties
{
・・・
[MaterialToggle] _Inverse ("Inverse", Float) = 0
・・・
}
fixed4 frag (v2f i) : SV_Target
{
・・・
col.a = inv - a * (inv * 2.0 - 1.0);
return col;
}実行結果
Division Size = 16、Width = 0.35、Direction(X, Y) = (1, 0)でシェーダを実行した結果は以下の通りです。
同じ条件でInverseにチェックを入れると以下のようになります。
また、Direction(X, Y) = (4, 3)とすると
このように、斜めに動きます。
中央から円が拡がるトランジション
中央から拡がるように円の大きさが変化するトランジションシェーダを作成しました。
shader
作成したシェーダは以下の通りです。
Shader "Transition/Transition_Cirlce_Spread"
{
Properties
{
_MainTex ("Texture", 2D) = "white" {}
[MaterialToggle] _Inverse ("Inverse", Float) = 0
_Div ("Division Size", Int) = 16
_Value ("Value", Range(0, 1)) = 0
}
SubShader
{
Tags { "RenderType"="Transparent" "RenderType"="Transparent" }
Blend SrcAlpha OneMinusSrcAlpha
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float2 uv : TEXCOORD0;
float4 vertex : SV_POSITION;
};
sampler2D _MainTex;
float4 _MainTex_ST;
int _Div;
float _Inverse;
float _Speed;
float _Value;
v2f vert (appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = TRANSFORM_TEX(v.uv, _MainTex);
return o;
}
//circle
float circle(float2 p){
return dot(p, p);
}
fixed4 frag (v2f i) : SV_Target
{
float inv = _Inverse;
float div = (float)_Div;
float2 st = i.uv * div + frac(div * 0.5 + 0.5);
float asp = _ScreenParams.y / _ScreenParams.x;
st.y *= asp;
st.y += (1.0 - frac(asp)) * (0.5 + floor(div * 0.5));
float2 i_st = floor(st) - floor(div * 0.5);
float2 f_st = frac(st) * 2.0 - 1.0;
float2 sm;
sm.x = floor(div * 0.5);
sm.y = floor(div * asp * 0.5 + 0.5);
float val = _Value * (length(sm) + 2.0);
float a = 1;
for(int i = -1; i <= 1; i++){
for(int j = -1; j <= 1; j++){
float v = val - length(i_st + float2(i, j));
float ci = circle(f_st - float2(2.0 * i, 2.0 * j));
a = min(a, step(v, ci));
//a = min(a, smoothstep(v - 0.01, v, ci));
}
}
fixed4 col = 0.0;
col.a = inv - a * (inv * 2.0 - 1.0);
return col;
}
ENDCG
}
}
}uv座標に分割数(_Div)を乗算するのは先ほどのシェーダと同様です。分割数が奇数の場合は最初の円が中央に配置されますが、偶数の場合は分割した領域の半分だけずれてしまいます。そのため、二項目を加算しています。分割数が8の時、stは0.5~8.5となります。
float2 st = i.uv * div + frac(div * 0.5 + 0.5);次に、縦方向の座標をアスペクト比で調整します。分割数が8、アスペクト比が4:3の時、st.y = 0.375~6.375となります。
float asp = _ScreenParams.y / _ScreenParams.x;
st.y *= asp;
float2 i_st = floor(st) - floor(div * 0.5);ただ、座標にアスペクト比を乗算しただけでは最初の円を画面中央に配置できません。以下の画像は上記コードで区切った座標を可視化したものです。
そこで、以下の値を加算することで円を画面中央に配置できるようにしました。分割数8の時st.yは1.5~7.5となります。よって、i_st.yは-3~3となります。
st.y *= asp;
st.y += (1.0 - frac(asp)) * (0.5 + floor(div * 0.5));
float2 i_st = floor(st) - floor(div * 0.5);また、先ほどのシェーダと同様に、円が領域からはみ出しても問題がないように処理をしています。i_stは中央を0とし縦(-x~x)と横(-y~y)の整数値となります。よって、lengthによってタイミングをずらすと、中央から拡がるようにそれぞれの円が大きくなります。
for(int i = -1; i <= 1; i++){
for(int j = -1; j <= 1; j++){
float v = val - length(i_st + float2(i, j));
float ci = circle(f_st - float2(2.0 * i, 2.0 * j), 0.0);
a = min(a, smoothstep(v - 0.01, v, ci));
}
}さらに、_Valが0~1の範囲に収まるよう処理を加えています。
float2 sm;
sm.x = floor(div * 0.5);
sm.y = floor(div * asp * 0.5 + 0.5);
float val = _Value * (length(sm) + 2.0);このシェーダにも先ほどと同様に反転させる処理を加えています。
Properties
{
・・・
[MaterialToggle] _Inverse ("Inverse", Float) = 0
・・・
}
fixed4 frag (v2f i) : SV_Target
{
・・・
col.a = inv - a * (inv * 2.0 - 1.0);
return col;
}実行結果
Division SIze = 16でシェーダを実行すると以下の結果が得られます。
また、Inverseにチェックを入れ、実行すると
となります。
-
前の記事

シェーダでトランジション(ノイズ) 2019.05.01
-
次の記事

ゲルストナー波(Gerstner Wave) 2019.05.25



























コメントを書く