シェーダでノイズ3(セルノイズ)
このノイズは細胞のように、区分けされた結果が得られるノイズです
セルラーノイズ
このノイズはあるピクセルから、ランダムに与えられた複数の点の中から一番近い点までの距離を出力するノイズです。
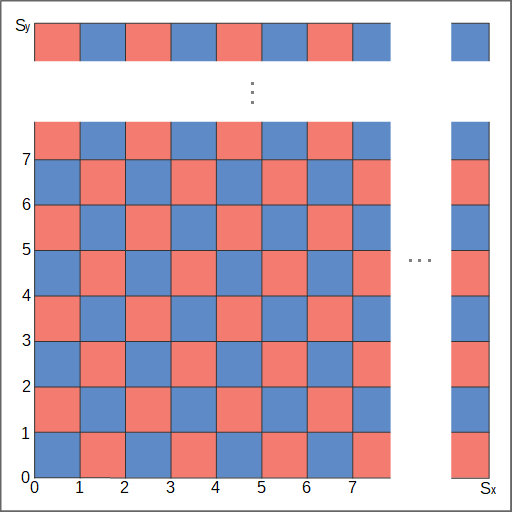
始めに、バリューノイズやパーリンノイズで行ったように、UV座標に定数を掛け、その値の小数部分を取り出すことで格子状に区切ります。
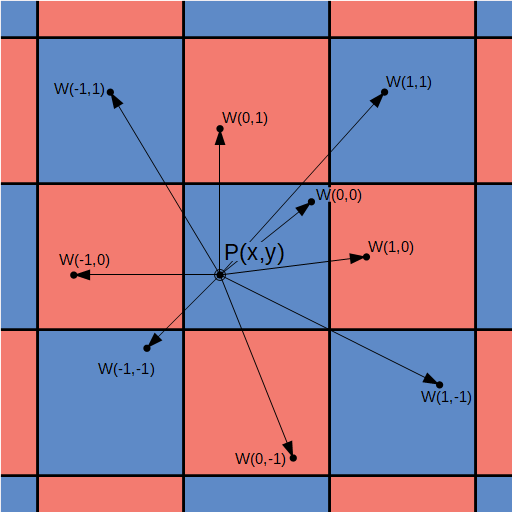
この格子ごとにランダムな点を決定します。次に、ピクセルから一番近いランダムな点までの距離を求めます。一番近い点は、あるピクセルが存在する格子ではなく、そのピクセルが存在する格子の周辺の格子に一番近い点が存在する可能性があります。そのため、ピクセルから一番近い点までの距離を求めるには、ピクセルが存在する格子とその周辺の格子、つまり、下図のように九か所の格子に存在する点までの距離を調べる必要があります。
そして、一番近いランダムな点までの距離を保存し、その距離を出力します。
shader
セルラーノイズの結果は以下の通りです。for文内でピクセルから九か所のランダムな点までの距離を調べつつ、min関数により一番近いランダムな点までの距離を記録しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
Shader "Noise/CellularNoise" { Properties { _MainTex ("Texture", 2D) = "white" {} _Seed ("Seed", Int) = 0 _SizeX ("SizeX", Int) = 1 _SizeY ("SizeY", Int) = 1 } SubShader { Tags { "RenderType"="Opaque" } LOD 100 Pass { CGPROGRAM #pragma vertex vert #pragma fragment frag #include "UnityCG.cginc" struct appdata { float4 vertex : POSITION; float2 uv : TEXCOORD0; }; struct v2f { float2 uv : TEXCOORD0; float4 vertex : SV_POSITION; }; sampler2D _MainTex; float4 _MainTex_ST; int _Seed; int _SizeX; int _SizeY; float2 rand(float2 st, int seed) { float2 s = float2(dot(st, float2(127.1, 311.7)) + seed, dot(st, float2(269.5, 183.3)) + seed); return frac(sin(s) * 43758.5453123); } v2f vert (appdata v) { v2f o; o.vertex = UnityObjectToClipPos(v.vertex); o.uv = TRANSFORM_TEX(v.uv, _MainTex); return o; } fixed4 frag (v2f i) : SV_Target { int seed = _Seed; float2 st = float2(i.uv.x * _SizeX, i.uv.y * _SizeY); float2 i_st = floor(st); float2 f_st = frac(st); float min_dist = 1; for(int j = -1; j <= 1; j++){ for(int k = -1; k <= 1; k++){ float2 n = float2(j, k); float2 p = rand(i_st + n, seed) + n; float dist = distance(f_st, p); min_dist = min(min_dist, dist); } } fixed4 col = min_dist; col.a = 1; return col; } ENDCG } } } |
実行結果
上記シェーダの実行結果は以下の通りです。細胞のように区分けわれたような結果が得られます。
ボロノイ図
ボロノイ図はピクセルから一番近いランダムな点に応じて領域を分けた図です。ボロノイ図を作成は、セルラーノイズを少し変更するだけで実現できます。
セルラーノイズではピクセルから一番近いランダムな点までの距離を以下のように求めていました。
|
1 |
min_dist = min(min_dist, dist); |
この部分をif文によって以下のように書き換えます。
|
1 2 3 4 |
if(dist < min_dist){ min_dist = dist; min_p = p; } |
if文に置き換えることで、一番近い距離だけでないく一番近いランダムな点の座標を保存できます。この座標と距離を利用することで色分けできます。
|
1 2 |
col = min_dist * 0.1; col.rg += min_p; |
また、座標と任意のベクトルの内積をとることで、グレースケールの結果が得られます。
|
1 |
col = dot(min_p, float2(0.3, 0.6)); |
shader
ボロノイ図を表示するシェーダは以下の通りです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 |
Shader "Noise/Voronoi" { Properties { _MainTex ("Texture", 2D) = "white" {} _Seed ("Seed", Int) = 0 _SizeX ("SizeX", Int) = 1 _SizeY ("SizeY", Int) = 1 } SubShader { Tags { "RenderType"="Opaque" } Pass { CGPROGRAM #pragma vertex vert #pragma fragment frag #include "UnityCG.cginc" struct appdata { float4 vertex : POSITION; float2 uv : TEXCOORD0; }; struct v2f { float2 uv : TEXCOORD0; float4 vertex : SV_POSITION; }; sampler2D _MainTex; float4 _MainTex_ST; int _Seed; int _SizeX; int _SizeY; float2 rand(float2 st, int seed) { float2 s = float2(dot(st, float2(127.1, 311.7)) + seed, dot(st, float2(269.5, 183.3)) + seed); return frac(sin(s) * 43758.5453123); } v2f vert (appdata v) { v2f o; o.vertex = UnityObjectToClipPos(v.vertex); o.uv = TRANSFORM_TEX(v.uv, _MainTex); return o; } fixed4 frag (v2f i) : SV_Target { int seed = _Seed; float2 st = float2(i.uv.x * _SizeX, i.uv.y * _SizeY); float2 i_st = floor(st); float2 f_st = frac(st); float min_dist = 1; float2 min_p; for(int j = -1; j <= 1; j++){ for(int k = -1; k <= 1; k++){ float2 n = float2(j, k); float2 p = rand(i_st + n, seed); float dist = distance(f_st, p + n); if(dist < min_dist){ min_dist = dist; min_p = p; } } } fixed4 col = min_dist; //グレースケール col = dot(min_p, float2(0.3, 0.6)); //カラー col = min_dist * 0.1; col.rg += min_p; col.a = 1; return col; } ENDCG } } } |
実行結果
上記シェーダの実行結果は以下の通りです。カラーで出力すると以下のようになります。
また、グレースケールで出力すると以下のようになります。
ボロノイ図の改良
ボロノイ図を描画する際には一番近い点までの距離を利用していましたが、二番目に近い点までの距離を利用することで他の結果を得ることができます。if文を以下のように変更することで二番目に近い点までの距離を保存します。
|
1 2 3 4 5 6 |
if(dist < min_dist){ t_dist = min_dist; min_dist = dist; }else if(dist < t_dist){ t_dist = dist; } |
これらの距離を利用することで、ボロノイ図とは違った結果が得られます。他には、ボロノイ図の境界線を描画するシェーダがここで紹介されています。
実行結果
一番近い点までの距離をF1、二番目に近い点までの距離をF2とします。これらを利用することで以下のような結果が得られます。
F2
F2-F1
F2*F1
参考サイト
-
前の記事
シェーダでノイズ2（パーリンノイズ） 2019.02.16
-
次の記事
HP残量によって色が変化するHPゲージ 2019.03.17