シェーダでテクスチャフィルタリング

2018.12.15
Unity
shader

　Unityでは画像のフィルタリングをImport Settings→Filter Modeから変更できます。シェーダで特に何もしない場合は、この設定に従って色の補間が行われます。ただ、前回記事（水中の屈折）でフィルタ処理を行う必要がありました。そこで、フィルタリングを行うシェーダを作成してみました。

1. ポイントフィルタ
- 1.1. シェーダ
- 1.2. 実行結果
2. バイリニアフィルタ
- 2.1. シェーダ
- 2.2. 実行結果

ポイントフィルタ

　ポイントフィルタはピクセルの色を決定する際に、色の合成を行うことなく一番近いテクセルの色をそのまま使用します。そのため、このフィルタではピクセルの中心を一番近いテクセルの中心へずらす処理が必要になります。この処理によって色の合成が行われなくなり、テクセルの色がそのまま出力されます。

　まずは、UV座標の横方向$u$について考えます。$u$はテクスチャの幅を$w$とすると

$$u=\frac{n}{w} (0\leq n \leq w)\tag{1}$$

と表せます。$n$を整数部分$n_{i}$と少数部分$n_{d}$に分けると

\begin{eqnarray} u=\frac{n_{i}+n_{d}}{w} \left\{ \begin{array}{l} (0\leq n_{i} \leq w) \\ (0\leq n_{d} \lt 1) \tag{2} \end{array} \right. \end{eqnarray}

となります。この式において、整数部分は任意のテクセルの端を示しており、小数部分はそのテクセルの端からの距離を示しています。

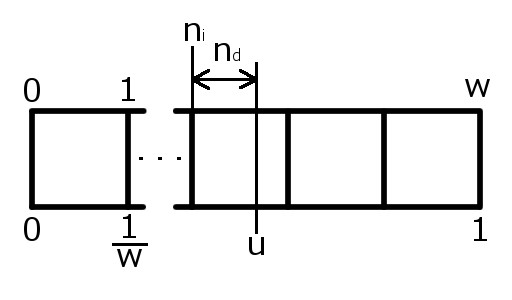
$n_{i}$に0.5を加算することでテクセルの中心へずらすことができます。この値をテクスチャの幅$w$で割り、UV座標へ変換することでテクセルの中心へUV座標をずらすことができます。よって、テクセルの中心を示す座標を$u_{t}$と置くと

$$u_{t}=\frac{n_{i}+0.5}{w} (0\leq n_{i} \leq w)\tag{3}$$

となる。式$(2)$より$n_{i}$は $$n_{i}=floor(uw)\tag{4}$$ と表せる。上式を式$(3)$へ代入すると

$$u_{t}=\frac{floor(uw)+0.5}{w}\tag{5}$$

となり、上式より$u_{t}$が求められます。縦方向も同様に求めることができます。よって、テクセルの中心座標$(u_{t},v_{t})$は $$(u_{t},v_{t})=\frac{floor\{(u,v)(w,h)\}+(0.5,0.5)}{(w,h)}\tag{6}$$ となります。この式によってシェーダでポイントフィルタをかけることができます。

シェーダ

　先ほど求めた式を使用して、ポイントフィルタをかけるシェーダを作成しました。テクスチャのFilter Modeがポイントフィルタ以外になっていないと効果はありません。PointFilterにチェックを入れるとポイントフィルタがかかります。

Shader "Unlit/PointFilter"
{
	Properties
	{
		_MainTex ("Texture", 2D) = "white" {}
		[MaterialToggle] _On ("PointFilter", Float) = 0
	}
	SubShader
	{
		Tags { "RenderType"="Opaque" }

		Pass
		{
			CGPROGRAM
			#pragma vertex vert
			#pragma fragment frag
			
			#include "UnityCG.cginc"

			struct appdata
			{
				float4 vertex : POSITION;
				float2 uv : TEXCOORD0;
			};

			struct v2f
			{
				float2 uv : TEXCOORD0;
				float4 vertex : SV_POSITION;
			};

			sampler2D _MainTex;
			float4 _MainTex_ST;
			float4 _MainTex_TexelSize;
			float _On;

			v2f vert (appdata v)
			{
				v2f o;
				o.vertex = UnityObjectToClipPos(v.vertex);
				o.uv = TRANSFORM_TEX(v.uv, _MainTex);
				UNITY_TRANSFER_FOG(o,o.vertex);
				return o;
			}
			
			fixed4 frag (v2f i) : SV_Target
			{
				float2 uv = (floor(i.uv * _MainTex_TexelSize.zw) + 0.5) * abs(_MainTex_TexelSize.xy) * _On;
				uv += i.uv * (1 - _On) ;
				fixed4 col = tex2D(_MainTex, uv);
				return col;
			}
			ENDCG
		}
	}
}

Shader "Unlit/PointFilter"

{

Properties

{

_MainTex ("Texture", 2D) = "white" {}

[MaterialToggle] _On ("PointFilter", Float) = 0

}

SubShader

{

Tags { "RenderType"="Opaque" }

Pass

{

CGPROGRAM

#pragma vertex vert

#pragma fragment frag

#include "UnityCG.cginc"

struct appdata

{

float4 vertex : POSITION;

float2 uv : TEXCOORD0;

};

struct v2f

{

float2 uv : TEXCOORD0;

float4 vertex : SV_POSITION;

};

sampler2D _MainTex;

float4 _MainTex_ST;

float4 _MainTex_TexelSize;

float _On;

v2f vert (appdata v)

{

v2f o;

o.vertex = UnityObjectToClipPos(v.vertex);

o.uv = TRANSFORM_TEX(v.uv, _MainTex);

UNITY_TRANSFER_FOG(o,o.vertex);

return o;

}

fixed4 frag (v2f i) : SV_Target

{

float2 uv = (floor(i.uv * _MainTex_TexelSize.zw) + 0.5) * abs(_MainTex_TexelSize.xy) * _On;

uv += i.uv * (1 - _On) ;

fixed4 col = tex2D(_MainTex, uv);

return col;

}

ENDCG

}

実行結果

　FilterModeをBilinearに設定し、そのまま出力した結果は以下のようになります。

この画像にシェーダでポイントフィルタをかけると、以下の結果が得られます。これより、ポイントフィルタがかかっていることがわかります。

バイリニアフィルタ

　バイニリアフィルタはピクセルの中心に近い4つのテクセルの色を、ピクセルの中心からテクセルの中心までの距離に応じて色を合成するフィルタです。

　最初に、合成する色を取得する方法を考えます。図に示すようにUV座標からそれぞれ半テクセルずらした場所の色を取得すれば中心に近い4つのテクセルの色を取得できます。

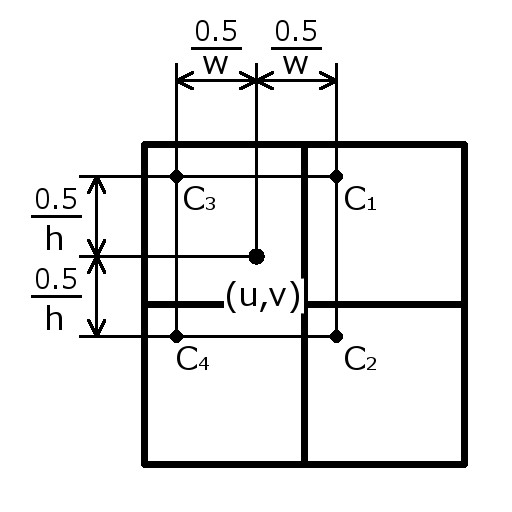
これをシェーダで記述すると以下のようになります。

float2 t = 0.5 * _MainTex_TexelSize.xy;
float4 c1 = tex2D(_MainTex, uv + float2(t.x, t.y));
float4 c2 = tex2D(_MainTex, uv + float2(t.x, -t.y));
float4 c3 = tex2D(_MainTex, uv + float2(-t.x, t.y));
float4 c4 = tex2D(_MainTex, uv + float2(-t.x, -t.y));

float2 t = 0.5 * _MainTex_TexelSize.xy;

float4 c1 = tex2D(_MainTex, uv + float2(t.x, t.y));

float4 c2 = tex2D(_MainTex, uv + float2(t.x, -t.y));

float4 c3 = tex2D(_MainTex, uv + float2(-t.x, t.y));

float4 c4 = tex2D(_MainTex, uv + float2(-t.x, -t.y));

　次に、取得した色を中心からの距離に応じて合成します。合成するにあたって、ピクセルの中心からテクセルの中心までの距離が必要になってきます。

　まずは、横方向のみについて考えます。ピクセルの中心からテクセルの中心までの距離を$d_x$とすると以下の図のようになります。

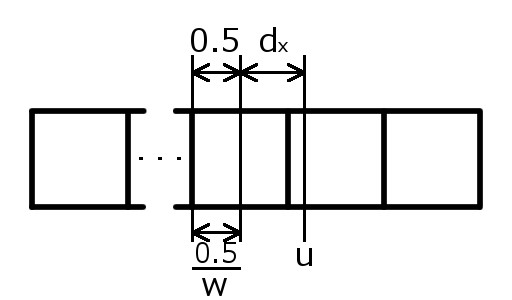
この図より、ピクセルの中心を$\frac{0.5}{w}$ずらすと以下の図のようになります。これより、ピクセルの中心からのテクセルの中心までの距離が、ピクセルの中心から$\frac{0.5}{w}$ずらした場所からテクセルの端の距離に変換できることがわかります。

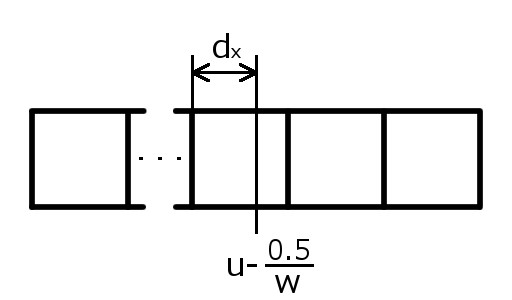
$d_x$はテクセルの端からの距離である式$(2)$の$n_{d}$となるので、ピクセルの中心からテクセルの中心までの距離は

$$d_x=n_{d}=frac\biggl\{(u-\frac{0.5}{w})w\biggl\}\tag{7}$$

より求めることができます。$d_x$は距離に応じて$0\leq d_x \lt 1$の値となるので、lerpによってピクセルの中心からの距離に応じた色の合成ができます。縦方向についても同様に求めることができます。よって

$$(d_x,d_y)=frac\biggl[\biggl\{(u,v)-\frac{(0.5,0.5)}{(w,h)}\biggl\}\tag{8}(w,h)\biggl]$$

となります。この式を利用し色の合成を行います。

シェーダ

　テクスチャのFilter ModeをPoint(no filter)に設定してください。Bilinearにチェックを入れるとバイリニアフィルタがかかります。

Shader "Unlit/Bilinear"
{
	Properties
	{
		_MainTex ("Texture", 2D) = "white" {}
		[MaterialToggle] _On ("Bilinear", Float) = 0
	}
	SubShader
	{
		Tags { "RenderType"="Opaque" }
		LOD 100

		Pass
		{
			CGPROGRAM
			#pragma vertex vert
			#pragma fragment frag
			
			#include "UnityCG.cginc"

			struct appdata
			{
				float4 vertex : POSITION;
				float2 uv : TEXCOORD0;
			};

			struct v2f
			{
				float2 uv : TEXCOORD0;
				float4 vertex : SV_POSITION;
			};

			sampler2D _MainTex;
			float4 _MainTex_ST;
			float4 _MainTex_TexelSize;

			float _On;
			
			v2f vert (appdata v)
			{
				v2f o;
				o.vertex = UnityObjectToClipPos(v.vertex);
				o.uv = TRANSFORM_TEX(v.uv, _MainTex);
				return o;
			}
			
			float4 Bilinearfilter(float2 uv)
			{
				float2 t = 0.5 * _MainTex_TexelSize.xy;
				float4 c1 = tex2D(_MainTex, uv + float2(t.x, t.y));
				float4 c2 = tex2D(_MainTex, uv + float2(t.x, -t.y));
				float4 c3 = tex2D(_MainTex, uv + float2(-t.x, t.y));
				float4 c4 = tex2D(_MainTex, uv + float2(-t.x, -t.y));

				float2 texPos = (uv - 0.5 * _MainTex_TexelSize.xy) * _MainTex_TexelSize.zw;

				float dx = frac(texPos.x);
				float dy = frac(texPos.y);

				float4 temp1 = lerp(c4, c2, dx);
				float4 temp2 = lerp(c3, c1, dx);

				return lerp(temp1, temp2, dy);
			}

			fixed4 frag (v2f i) : SV_Target
			{
				fixed4 col = tex2D(_MainTex, i.uv);
				col = col * (1 - _On) + Bilinearfilter(i.uv) * _On;
				return col;
			}
			ENDCG
		}
	}
}

Shader "Unlit/Bilinear"

{

Properties

{

_MainTex ("Texture", 2D) = "white" {}

[MaterialToggle] _On ("Bilinear", Float) = 0

}

SubShader

{

Tags { "RenderType"="Opaque" }

LOD 100

Pass

{

CGPROGRAM

#pragma vertex vert

#pragma fragment frag

#include "UnityCG.cginc"

struct appdata

{

float4 vertex : POSITION;

float2 uv : TEXCOORD0;

};

struct v2f

{

float2 uv : TEXCOORD0;

float4 vertex : SV_POSITION;

};

sampler2D _MainTex;

float4 _MainTex_ST;

float4 _MainTex_TexelSize;

float _On;

v2f vert (appdata v)

{

v2f o;

o.vertex = UnityObjectToClipPos(v.vertex);

o.uv = TRANSFORM_TEX(v.uv, _MainTex);

return o;

}

float4 Bilinearfilter(float2 uv)

{

float2 t = 0.5 * _MainTex_TexelSize.xy;

float4 c1 = tex2D(_MainTex, uv + float2(t.x, t.y));

float4 c2 = tex2D(_MainTex, uv + float2(t.x, -t.y));

float4 c3 = tex2D(_MainTex, uv + float2(-t.x, t.y));

float4 c4 = tex2D(_MainTex, uv + float2(-t.x, -t.y));

float2 texPos = (uv - 0.5 * _MainTex_TexelSize.xy) * _MainTex_TexelSize.zw;

float dx = frac(texPos.x);

float dy = frac(texPos.y);

float4 temp1 = lerp(c4, c2, dx);

float4 temp2 = lerp(c3, c1, dx);

return lerp(temp1, temp2, dy);

}

fixed4 frag (v2f i) : SV_Target

{

fixed4 col = tex2D(_MainTex, i.uv);

col = col * (1 - _On) + Bilinearfilter(i.uv) * _On;

return col;

}

ENDCG

}

実行結果

　FilterModeをPoint(no filter)に設定し、そのまま出力した結果は以下のようになります。

この画像にシェーダでバイリニアフィルタをかけると、以下の結果が得られます。これより、バイリニアフィルタがかかっていることがわかります。

前の記事

水中の屈折(shader) 2018.12.08
次の記事

UI要素をScriptから作成 2019.01.23

シェーダでテクスチャフィルタリング

ポイントフィルタ

シェーダ

実行結果

バイリニアフィルタ

シェーダ

実行結果

水中の屈折(shader) 2018.12.08

UI要素をScriptから作成 2019.01.23